题目内容
抛物线x2=ay(a>0)的准线l与y轴交于点P,若l绕点P以每秒A.1 B.2 C.3 D.4
C 设切点为(x0,y0),∵y=![]() x2,∴y′=
x2,∴y′=![]() x.∴斜率为
x.∴斜率为![]() x0;
x0;
又根据切点(x0,![]() x02),点P(0,
x02),点P(0,![]() ),
),
得斜率为 ,∴
,∴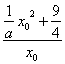 =
=![]() `x0.∴x02=
`x0.∴x02=![]() .根据题意x0>0,∴x0=
.根据题意x0>0,∴x0=![]() .
.
∴斜率为1.∴t秒钟转过了![]() .∴t=
.∴t=![]() =3.
=3.

练习册系列答案
相关题目
题目内容
抛物线x2=ay(a>0)的准线l与y轴交于点P,若l绕点P以每秒A.1 B.2 C.3 D.4
C 设切点为(x0,y0),∵y=![]() x2,∴y′=
x2,∴y′=![]() x.∴斜率为
x.∴斜率为![]() x0;
x0;
又根据切点(x0,![]() x02),点P(0,
x02),点P(0,![]() ),
),
得斜率为 ,∴
,∴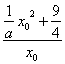 =
=![]() `x0.∴x02=
`x0.∴x02=![]() .根据题意x0>0,∴x0=
.根据题意x0>0,∴x0=![]() .
.
∴斜率为1.∴t秒钟转过了![]() .∴t=
.∴t=![]() =3.
=3.
