题目内容
（本小题满分12分）已知函数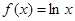
，若存在
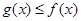恒成立，则称
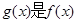的一个“下界函数”.
（I）如果函数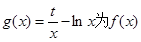
的一个“下界函数”，求实数t的取值范围；
（II）设函数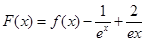
，试问函数F(x)是否存在零点？若存在，求出零点个数；若不存在，请说明理由.
【答案】
(I)解析：
恒成立，即
恒成立.
令
由
得
， （3分）
当
时，
在
上是减函数，当
时，
在
上是增函数，
（6分）
（2）解法一：由（1）知
，① （9分）
令
，则
由
得
则当
时，
在
上是减函数，
时，在
上是增函数.
，②
，
①②中等号取到的条件不同，
函数
不存在零点。
解法二：假设F(x)存在零点，即
上有解
∴
令
若
是减函数
若
是增函数
再令
若
是增函数
若
是减函数
又∵两个函数取到最值的条件不同
∴函数F(x)不存在零点.
【解析】略
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
