题目内容
(本小题满分12分)已知函数 的图象与
的图象与 轴分别相交于点
轴分别相交于点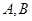 两点,向量
两点,向量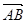
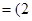 ,
,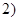 ,又函数
,又函数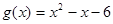 ,且
,且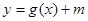 的值域是
的值域是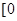 ,
,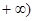 。
。
(1)求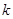 ,
, 及
及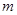 的值;(2)当
的值;(2)当 满足
满足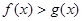 时,求函数
时,求函数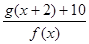 的最小值。
的最小值。
(1) (2)3
(2)3
解析试题分析:(1)因为函数 的图象与
的图象与 轴分别相交于点
轴分别相交于点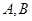 两点,
两点,
分别令 得
得 ,
, ,则
,则 ,
,
又因为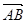
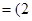 ,
,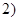 ,
, ……4分
……4分
又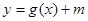
 的值域是
的值域是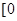 ,
,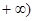 ,
,
所以 ,解得
,解得 ,
,
所以 . ……6分
. ……6分

所以 ,
,
因为 ,所以
,所以 4,
4,
当且仅当 时等号成立,
时等号成立,
所以 时,
时,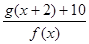 的最小值是3. ……12分
的最小值是3. ……12分
考点:本小题主要考查直线的交点、二次函数的值域以及利用基本不等式求最值,考查学生对问题的转化能力以及运算求解能力.
点评:利用基本不等式求最值时,一正二定三相等三个条件缺一不可,而且还要写清楚取等号的条件.

练习册系列答案
相关题目
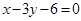 ,若点
,若点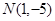 在直线AD上.
在直线AD上.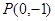 的直线
的直线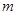 与ABCD外接圆相交于A、B两点,若
与ABCD外接圆相交于A、B两点,若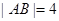 ,求直线m的方程.
,求直线m的方程.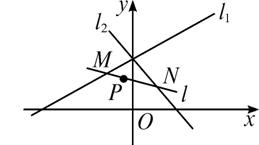
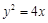 的焦点为F,
的焦点为F,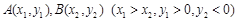 在抛物线上,且存在实数
在抛物线上,且存在实数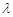 ,使
,使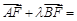
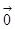 ,
,
 相切的切线方程.
相切的切线方程. 经过点P(5,5)且和圆C:
经过点P(5,5)且和圆C:  ,求
,求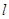 //AB,与AC,BC依次交于E,F,
//AB,与AC,BC依次交于E,F,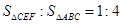 .求
.求 一条光线从点P(6,4)射出,经y轴反射后经过点Q(3,10),求入射光线和反射光线所在直线方程。 (12分)
一条光线从点P(6,4)射出,经y轴反射后经过点Q(3,10),求入射光线和反射光线所在直线方程。 (12分)