题目内容
函数f(x)=x|x+a|+b是奇函数的充要条件是( )
| A.ab="0" | B.a+b=0 | C.a=b | D.a2+b2=0 |
D
解析试题分析:是奇函数有f(0)=0,得b=0,f(-1)=-f(1),得a=0,∴答案是D.
考点:函数的奇偶性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数
 ,数列
,数列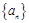 满足
满足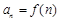
 ,且数列
,且数列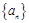 是递增数列,则实数
是递增数列,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知函数① ②
② ,③
,③ ,④
,④ 的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
的部分图象如下,但顺序被打乱,则按照图象从左到右的顺序,对应的函数序号正确的一组是( )
| A.①④②③ | B.①④③② | C.④①②③ | D.③④②① |
定义域为 的函数
的函数 满足
满足 ,当
,当 时,
时, 若当
若当 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B.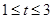 | C. | D. |
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
函数 为偶函数,且在
为偶函数,且在 单调递增,则
单调递增,则 的解集为( )
的解集为( )
A. | B. |
C. | D. |
 的部分图象可能是( )
的部分图象可能是( )
 ,则下列函数的图象错误的是( )
,则下列函数的图象错误的是( )
 的图象可能是( )
的图象可能是( )