题目内容
8.解方程组:$\left\{\begin{array}{l}{a=-b(a-1)}\\{\frac{4}{\sqrt{{a}^{2}+{b}^{2}}}=\frac{|b|}{\sqrt{(a-1)^{2}+1}}}\end{array}\right.$.分析 由a=-b(a-1)得a-1=$-\frac{a}{b}$代入第二个式子进行化简求解即可.
解答 解:由a=-b(a-1)得a-1=$-\frac{a}{b}$代入第二个式子得$\frac{4}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{|b|}{\sqrt{(-\frac{a}{b})^{2}+1}}$=$\frac{{b}^{2}}{\sqrt{{a}^{2}+\sqrt{{b}^{2}}}}$,
即b2=4,
则b=2或b=-2,
若b=2,则a=-2(a-1),得a=$\frac{2}{3}$,
若b=-2,则a=2(a-1),得a=2,
即方程组的解为$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=2}\end{array}\right.$或$\left\{\begin{array}{l}{a=2}\\{b=-2}\end{array}\right.$.
点评 本题主要考查方程组的求解,利用第一个式子求出a-1=$-\frac{a}{b}$代入第二个式子进行化简是解决本题的关键.

练习册系列答案
相关题目
13. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )| A. | 在棱AD上存在点M,使AD⊥平面PMB | B. | 异面直线AD与PB所成的角为90° | ||
| C. | 二面角P-BC-A的大小为45° | D. | BD⊥平面PAC |
19.函数f(x)=x•e-x的单调递增区间是( )
| A. | [-1,+∞) | B. | (-∞,1] | C. | [-1,1] | D. | (-∞,-1] |
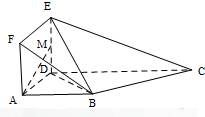 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.