题目内容
在侧棱长为a的正四棱锥中,棱锥的体积最大时底面边长为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、a |
分析:本题探究棱锥体积最大时底面边的取值,故可先设底面边长为x,用x表示出棱锥的体积,即得体积关于底面边长的函数,利用函数的相关知识求出体积最大时边长的值即可.
解答:解:设底面边长为x,因为侧棱长为a的正四棱锥,故底面对角线长为
x,底面面积是x2
故棱锥的高为
棱锥的体积V=
×
× x2
用导数法对函数研究知,当x=
a时,棱锥的体积V=
×
× x2取到最大值.
故选A
| 2 |
故棱锥的高为
a2-(
|
棱锥的体积V=
| 1 |
| 3 |
a2-(
|
用导数法对函数研究知,当x=
2
| ||
| 3 |
| 1 |
| 3 |
a2-(
|
故选A
点评:本题考点是棱柱、棱锥、棱台的体积,考查利用棱锥的体积公式建立起关于体积的函数模型,利用函数的性质求出函数的最值及取到最值时底边的长.

练习册系列答案
相关题目
侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形,且四个顶点都在一个球面上,则该球的表面积为( )
A、
| ||
| B、2πa2 | ||
C、
| ||
| D、3πa2 |
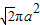
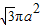
 a
a a
a a
a