题目内容
已知函数f(x)=ax2+2ln(1-x)(a∈R),且f(x)在[-3,-2)上是增函数,则实数a的取值范围是
- A.

- B.

- C.

- D.

D
分析:求出函数的导数,利用导数在[-3,-2)恒为正,通过二次函数的最值,即可求出实数a的取值范围
解答:求导函数,可得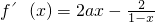
由题意得f′(x)≥0对一切x∈[-3,-2)恒成立,
∴a≤ =
=
当x∈[-3,-2)时,-(x- )2+
)2+ <-6,
<-6,
∴ >-
>- .故a≤-
.故a≤-
故选D.
点评:本题考查求函数的导数以及函数的最值问题,体现转化的数学思想,考查了二次函数在定区间上的最值问题,恒成立问题,属中档题.
分析:求出函数的导数,利用导数在[-3,-2)恒为正,通过二次函数的最值,即可求出实数a的取值范围
解答:求导函数,可得
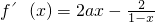
由题意得f′(x)≥0对一切x∈[-3,-2)恒成立,
∴a≤
 =
=
当x∈[-3,-2)时,-(x-
 )2+
)2+ <-6,
<-6,∴
 >-
>- .故a≤-
.故a≤-
故选D.
点评:本题考查求函数的导数以及函数的最值问题,体现转化的数学思想,考查了二次函数在定区间上的最值问题,恒成立问题,属中档题.

练习册系列答案
相关题目