题目内容
已知集合 ,
, .
.
(1)求集合 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(1)  ;(2)
;(2) .
.
解析试题分析:(1)解分式不等式一般是把分式不等式转化为整式不等式来解,先把分式不等式化为 (或
(或 )(注意使
)(注意使 ,
, 中各因式里
中各因式里 的最高次项系数为正),然后等价转化为整式不等式
的最高次项系数为正),然后等价转化为整式不等式 (或
(或 ),但如果不等式是
),但如果不等式是 (或
(或 ),转化后注意
),转化后注意 .本题中不等式
.本题中不等式 等价转化为
等价转化为 ;(2)注意结论
;(2)注意结论


 的区别.
的区别.
试题解析:解 (1)因为 ,所以
,所以 .
.
解得  ,∴集合
,∴集合 .
.
(2)因为 ,所以
,所以
解得 所以
所以 .
.
考点:(1)分式不等式的解法;(2)子集的概念.

练习册系列答案
相关题目
已知集合 ,
, ,则
,则 ( )
( )
A. | B. |
C. | D. |
已知集合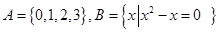 ,则集合
,则集合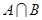 =( )
=( )
A.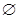 | B.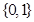 | C.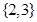 | D.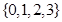 |
已知 ,则
,则 ( )
( )
| A.-2 | B.-6 | C.2 | D.一2或-6 |
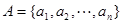 (n∈N*,n≥3),定义集合
(n∈N*,n≥3),定义集合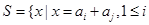
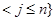 ,记集合S中的元素个数为S(A).(1)若集合A={1,2,3,4},则S(A)=______.
,记集合S中的元素个数为S(A).(1)若集合A={1,2,3,4},则S(A)=______. ;②
;② ;③
;③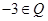 ;④
;④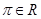 .
. ,集合
,集合 ,
, .
.
 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. A,求实数m的取值范围;
A,求实数m的取值范围; ,集合
,集合
 ,求集合
,求集合 ; (2)若
; (2)若 ,求实数
,求实数 的取值范围
的取值范围