题目内容
设函数f(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:f(x)在区间( ,1)内存在唯一零点;
,1)内存在唯一零点;
(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,求b的取值范围.
(1)设n≥2,b=1,c=-1,证明:f(x)在区间(
 ,1)内存在唯一零点;
,1)内存在唯一零点;(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,求b的取值范围.
(1)见解析 (2)最小值为-6,最大值为0. (3)-2≤b≤2
解:(1)当b=1,c=-1,n≥2时,f(x)=xn+x-1,
∵f
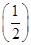 f(1)=
f(1)=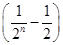 ×1<0,
×1<0,∴f(x)在(
 ,1)内存在零点.
,1)内存在零点.又∵当x∈(
 ,1)时,f′(x)=nxn-1+1>0,
,1)时,f′(x)=nxn-1+1>0,∴f(x)在区间(
 ,1)内单调递增,
,1)内单调递增,∴f(x)在(
 ,1)内存在唯一的零点.
,1)内存在唯一的零点.(2)依题意知

∴
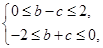 .
.画出可行域可知b+3c在点(0,-2)处取得最小值-6.在点(0,0)处取得最大值0,因而b+3c的最小值为-6,最大值为0.
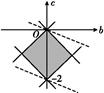
(3)当n=2时,f(x)=x2+bx+c,
对任意x1,x2∈[-1,1]都有|f(x1)-f(x2)|≤4等价于f(x)在[-1,1]上的最大值与最小值之差M≤4,据此分类讨论如下:
若
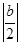 >1,即|b|>2时,
>1,即|b|>2时,M=|f(1)-f(-1)|=2|b|>4与题设矛盾.
若-1≤-
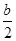 <0,即0<b≤2时,
<0,即0<b≤2时,M=f(1)-f(-
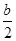 )=(
)=(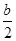 +1)2≤4恒成立.
+1)2≤4恒成立.若0≤-
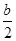 ≤1,即-2≤b≤0时,
≤1,即-2≤b≤0时,M=f(-1)-f(-
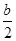 )=(
)=(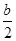 -1)2≤4恒成立.
-1)2≤4恒成立.综上可知,-2≤b≤2.

练习册系列答案
相关题目
 .
. ∈A,
∈A,
 A.
A. ,若存在
,若存在 ,使得任意
,使得任意 恒成立,且两边等号能取到,则
恒成立,且两边等号能取到,则 的最小值为 .
的最小值为 . 恒成立,则n的最大值为( ).
恒成立,则n的最大值为( ). >b-
>b- 同时成立,则ab应满足的条件是 .
同时成立,则ab应满足的条件是 .  ”的 ( )
”的 ( ) +
+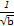 +
+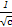 ≤a+b+c”的( )
≤a+b+c”的( )