Question

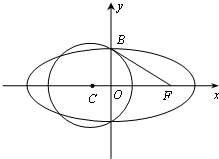（2010•深圳二模）已知圆C：（x+t）²+y²=5（t＞0）和椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）的一个公共点为B（0，2）．F为椭圆E的右焦点，直线BF与圆C相切于点B．
（Ⅰ）求t值和椭圆E的方程；
（Ⅱ）圆C上是否存在点M，使△MBF为等腰三角形？若存在，求出点M的坐标．

Answer 1

分析：（Ⅰ）由题可知，b=2，根据直线BF与圆C相切于点B，可求t=1，利用BC²+BF²=CF²，设F（c，0），则有(

5

)2+(22+c2)=(1+c)2，从而可求c=4，利用a²=b²+c²，b=2，可得a²=20，从而可求椭圆E的方程；
（Ⅱ）假设存在点M（x，y），使△MBF为等腰三角形，则M（x，y）点满足（x+1）²+y²=5…①，
下面分三种情况讨论：（1）BM=BF；（2）MB=MF；（3）FM=FB，即可求解

解答：解：（Ⅰ）由题可知，b=2…（1分）
∵C（-t，0），B（0，2），∴BC=

t2+22

=

5

，∴t=±1，又t＞0，∴t=1…（3分）
∵BF为圆C的切线，∴BC⊥BF，∴BC²+BF²=CF²，
设F（c，0），则有(

5

)2+(22+c2)=(1+c)2，∴c=4，…（5分）
又a²=b²+c²，b=2，∴a²=20，
所以椭圆E的方程为

x2

20

+

y2

4

=1…（6分）
（Ⅱ）假设存在点M（x，y），使△MBF为等腰三角形，
则M（x，y）点满足（x+1）²+y²=5…①，…（7分）
下面分三种情况讨论：
（1）当BM=BF时，
有

x2+(y-2)2

=

20

，即x²+（y-2）²=20…②
由①②联立得：

x=-2 y=-2

，∴M（-2，-2）…（9分）
（2）当MB=MF时，
有

x2+(y-2)2

=

(x-4)2+y2

，即2x-y=3…③
由①③联立得：

x=1 y=-1

，∴M（1，-1）…（11分）
（3）当FM=FB时，
有

(x-4)2+y2

=

20

，即x²+y²-8x-4=0…④
由①④联立得：

x=0 y=±2

，又B（0，2），∴M（0，-2）…（13分）
综上，圆C上存在点M（-2，-2）或M（1，-1）或M（0，-2），使△MBF为等腰三角形．    …（14分）

点评：本题以圆与椭圆为载体，考查椭圆的标准方程，考查是否存在性问题，注意分类讨论．