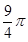题目内容
已知:过球面上A,B,C三点的截面和球心的距离是球半径的 ,且
,且 ,
, ,则球的表面积是( )
,则球的表面积是( )A.81π*
B.9π
C.

D.

【答案】分析:根据边长知△ABC是RT△,则球心的射影为斜边的中点,再由勾股定理求得球的半径,最后利用球的表面积公式即可.
解答:解:根据题意△ABC是RT△,且斜边上的中线长为 ,
,
又∵球心的射影为斜边的中点,
设球的半径为r,则有
∴
∴S球=4πr2=9π
故选B.
点评:本题主要考查直角三角形中线定理及球的基本性质.解答关键是构造直角三角形求解球的半径.
解答:解:根据题意△ABC是RT△,且斜边上的中线长为
 ,
,又∵球心的射影为斜边的中点,
设球的半径为r,则有

∴

∴S球=4πr2=9π
故选B.
点评:本题主要考查直角三角形中线定理及球的基本性质.解答关键是构造直角三角形求解球的半径.

练习册系列答案
相关题目
已知:过球面上A,B,C三点的截面和球心的距离是球半径的
,且|AB|=2
,
•
=0,则球的表面积是( )
| 1 |
| 3 |
| 2 |
| AC |
| BC |
| A、81π* | ||
| B、9π | ||
C、
| ||
D、
|
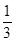 ,且
,且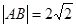 ,
, 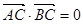 ,则球的表面积是( )
,则球的表面积是( )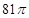 (B)
(B)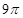 (C)
(C)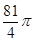 (D)
(D)