题目内容
(本题满分14分)
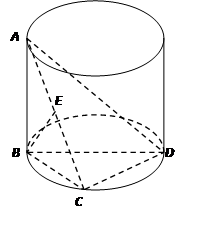
如图,已知平面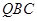 与直线
与直线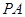 均垂直于
均垂直于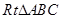 所在平面,且
所在平面,且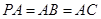 ,
,
(Ⅰ)求证: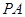
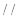 平面
平面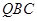 ;
;
(Ⅱ)若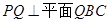 ,求
,求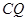 与平面
与平面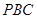 所成角的正弦值.
所成角的正弦值.
(Ⅰ)只需证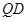 ∥
∥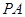 ;(Ⅱ)
;(Ⅱ)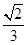 。
。
解析试题分析:(Ⅰ)证明:过点 作
作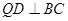 于点
于点 ,
,
∵平面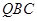 ⊥平面
⊥平面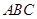 ,∴
,∴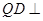 平面
平面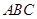 ……2分
……2分
又∵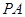 ⊥平面
⊥平面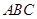
∴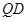 ∥
∥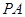 , ………………2分
, ………………2分
又∵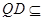 平面
平面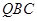
∴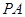 ∥平面
∥平面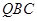 ………………6分
………………6分
(Ⅱ)∵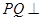 平面
平面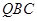 ∴
∴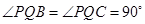 ,又∵
,又∵ ∴
∴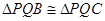 ∴
∴ ………………8分
………………8分
∴点 是
是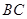 的中点,连结
的中点,连结 ,则
,则
∴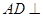 平面
平面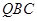 ∴
∴ ∥
∥ ,
,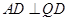
∴四边形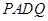 是矩形 ………………10分
是矩形 ………………10分
设 ,得:
,得: ,
,
又∵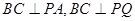 ,∴
,∴ ,
,
从而 ,过
,过 作
作 于点
于点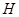 ,则:
,则:
∴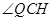 是
是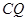 与平面
与平面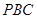 所成角 ………………………………………………12分
所成角 ………………………………………………12分
∴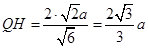 ,
,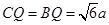

∴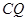 与平面
与平面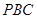 所成角的正弦值为
所成角的正弦值为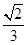 …………………………14分
…………………………14分
考点:面面垂直的性质定理;线面平行的判定定理;线面垂直的性质定理;直线与平面所成的角。
点评:本题主要考查了线面平行的证明和直线与平面所成的角,属立体几何中的常考题型,较难.本题也可以用向量法来做:用向量法解题的关键是;首先正确的建立空间直角坐标系,正确求解平面的一个法向量。注意计算要仔细、认真。

练习册系列答案
相关题目
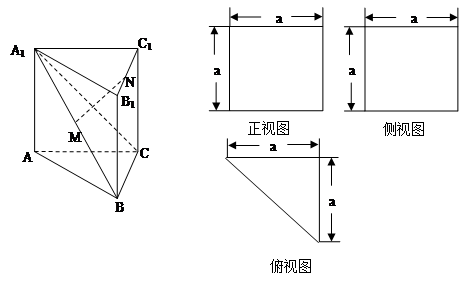
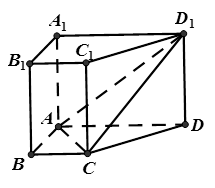
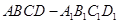 是棱长为
是棱长为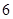 的正方体,
的正方体, 、
、 分别是棱
分别是棱 、
、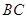 上的动点,且
上的动点,且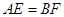 .
.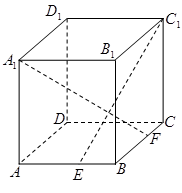
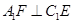 ;
;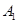 、
、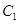 共面时,求:面
共面时,求:面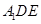 与面
与面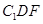 所成二面角的余弦值.
所成二面角的余弦值.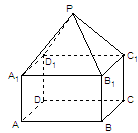
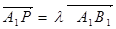
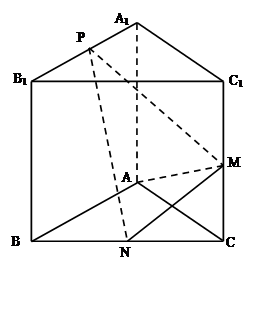
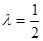 ,求直线AA1与平面PMN所成角的正弦值.
,求直线AA1与平面PMN所成角的正弦值.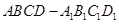 中,
中,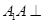 面
面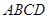 ,底面
,底面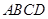 是直角梯形,
是直角梯形,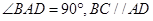 ,
,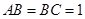 ,
,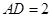 ,异面直线
,异面直线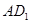 与
与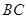 所成角为
所成角为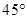 .
.
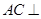 平面
平面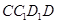 ;
;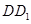 与平面
与平面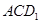 所成角的正弦值.
所成角的正弦值.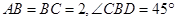 .
.
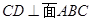 ;
;