Question

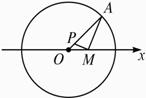
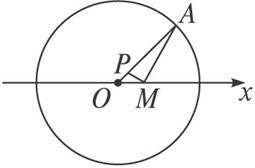
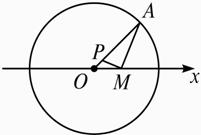
设M是定圆O内一定点，任作半径OA，连结MA，自M作MP⊥MA交OA于P，求P点的轨迹方程.

Answer 1

解:以O为极点，射线OM为极轴，建立极坐标系,如图.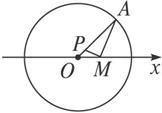

设定圆O的半径为r，OM=a，P(ρ,θ)是轨迹上任意一点.

∵MP⊥MA，∴|MA|²+|MP|²=|PA|²，由余弦定理可知|MA|²=a²+r²-2arcosθ，|MP|²=a²+ρ²-2aρcosθ,而|PA|=r-ρ，由此可得

a²+r²-2arcosθ+a²+ρ²-2aρcosθ=(r-ρ)²，整理化简，得ρ=.