题目内容
已知函数f(x)=3sin(2x+| π | 3 |
(Ⅰ)用“五点法”作出它在一个周期上的简图;
(Ⅱ)指出这个函数的振幅、频率和初相;
(Ⅲ)指出这个函数的单调区间.
分析:(Ⅰ)根据“五点法”作图的步骤,我们令相位角 2x+
分别等0,
,π,
,2π,并求出对应的x,y值,描出五点后,用平滑曲线连接后,即可得到函数 y=3sin(2x+
)的一个周期简图
(Ⅱ)根据图象可知函数的振幅,求出周期,再取倒数可知频率.
(Ⅲ)根据图象可知函数函数的单调区间.
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 3 |
(Ⅱ)根据图象可知函数的振幅,求出周期,再取倒数可知频率.
(Ⅲ)根据图象可知函数函数的单调区间.
解答:解:(Ⅰ)列表:
函数函数 y=3sin(2x+
)的在区间[-
,
]上的图象如下图所示:
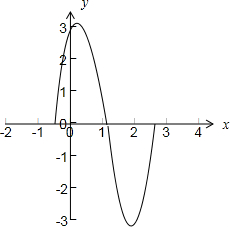
(Ⅱ)由图可知函数的振幅A=3,频率f=
=
=
.初相为
(Ⅲ)单调增区间为[kπ-
π,kπ+
](k∈Z);单调减区间为[kπ+
,kπ+
π](k∈Z).
2x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
y=3sin(2x+
|
0 | 3 | 0 | -3 | 0 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |

(Ⅱ)由图可知函数的振幅A=3,频率f=
| 1 |
| T |
| 2 |
| 2π |
| 1 |
| π |
| π |
| 3 |
(Ⅲ)单调增区间为[kπ-
| 5 |
| 12 |
| π |
| 12 |
| π |
| 12 |
| 7 |
| 12 |
点评:本题考查的知识点是五点法作函数y=Asin(ωx+φ)的图象,函数y=Asin(ωx+φ)的振幅,频率,单调区间,初相等性质.其中利用“五点法”画出函数的简图,并根据函数的直观性作答是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目