题目内容
【题目】四面体 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,则此四面体外接球的表面积为
,则此四面体外接球的表面积为 ![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
分析:由△BCD中,CB=DB=2,∠CBD=60°,可知△BCD是等边三角形,∠ABC=∠ABD=60°,可得AD=AC=![]() ,求出底面△BCD的外接圆半径r=
,求出底面△BCD的外接圆半径r=![]() .利用球心到圆心构造直角三角形即可求解外接球R.
.利用球心到圆心构造直角三角形即可求解外接球R.
详解:
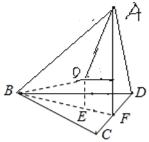
由题意,△BCD中,CB=DB=2,∠CBD=60°,
可知△BCD是等边三角形,BF=![]()
∴△BCD的外接圆半径r=![]() =BE,FE=
=BE,FE=![]()
∵∠ABC=∠ABD=60°,可得AD=AC=![]() ,
,
可得AF=![]()
∴AF⊥FB
∴AF⊥BCD,
∴四面体A﹣BCD高为AF=![]() .
.
设:外接球R,O为球心,OE=m
可得:r2+m2=R2……①,
(![]() )2+EF2=R2……②
)2+EF2=R2……②
由①②解得:R=![]() .
.
四面体外接球的表面积:S=4πR2=![]() .
.
故选:A.

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目


