题目内容
已知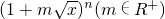 展开式的二项式系数之和为256,展开式中含x项的系数为112.
展开式的二项式系数之和为256,展开式中含x项的系数为112.
(Ⅰ)求m、n的值;
(Ⅱ)求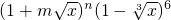 展开式中含x2项的系数.
展开式中含x2项的系数.
解:(Ⅰ)二项式系数之和为2n=256,可得n=8;…2分
设含x项为第r+1项,则Tr+1=
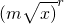 =
= mr
mr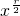 …3分
…3分
故 =1,即r=2,…4分
=1,即r=2,…4分
则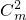 m2=112,解得m=±2…6分
m2=112,解得m=±2…6分
∵m∈R+,
∴m=2…7分
(Ⅱ)∵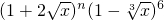 展开式的通项为
展开式的通项为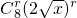 •
•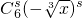 ,即
,即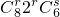
 (其中r=0,1,2,…8;s=0,2,…6),…9分
(其中r=0,1,2,…8;s=0,2,…6),…9分
令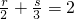 ,则3r+2s=12…10分
,则3r+2s=12…10分
∴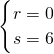 或
或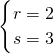 或
或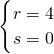 …12分
…12分
∴x2的系数为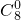 (-1)6+
(-1)6+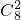 22
22 (-1)3+
(-1)3+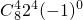 =-1119…14分
=-1119…14分
分析:(Ⅰ)由二项式系数之和为2n=256,可得n,再由二项展开式的通项公式结合含x项的系数为112可求的n的值;
(Ⅱ)由二项展开式的通项公式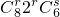
 可含求得x2项的系数.
可含求得x2项的系数.
点评:本题考查二项式定理的应用,着重考查二项展开式的通项公式的应用,注重转化与方程思想的运用,属于中档题.
设含x项为第r+1项,则Tr+1=

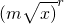 =
= mr
mr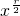 …3分
…3分故
 =1,即r=2,…4分
=1,即r=2,…4分则
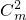 m2=112,解得m=±2…6分
m2=112,解得m=±2…6分∵m∈R+,
∴m=2…7分
(Ⅱ)∵
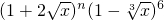 展开式的通项为
展开式的通项为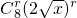 •
•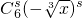 ,即
,即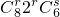
 (其中r=0,1,2,…8;s=0,2,…6),…9分
(其中r=0,1,2,…8;s=0,2,…6),…9分令
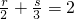 ,则3r+2s=12…10分
,则3r+2s=12…10分∴
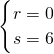 或
或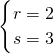 或
或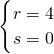 …12分
…12分∴x2的系数为
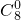 (-1)6+
(-1)6+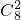 22
22 (-1)3+
(-1)3+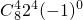 =-1119…14分
=-1119…14分分析:(Ⅰ)由二项式系数之和为2n=256,可得n,再由二项展开式的通项公式结合含x项的系数为112可求的n的值;
(Ⅱ)由二项展开式的通项公式
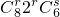
 可含求得x2项的系数.
可含求得x2项的系数.点评:本题考查二项式定理的应用,着重考查二项展开式的通项公式的应用,注重转化与方程思想的运用,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目