题目内容
已知数列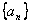 满足
满足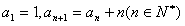 ,数列
,数列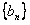 满足
满足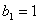 ,
,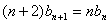 (n∈N* ),数列
(n∈N* ),数列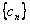 满足
满足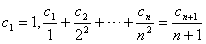 。
。
(1)求数列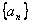 、
、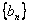 的通项公式;
的通项公式;
(2)求数列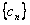 的通项公式;
的通项公式;
(3)是否存在正整数k,使得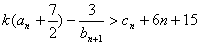 对一切
对一切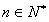 恒成立,若存在求k的最小值;若不存在请说明理由。
恒成立,若存在求k的最小值;若不存在请说明理由。
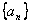 满足
满足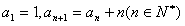 ,数列
,数列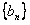 满足
满足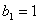 ,
,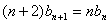 (n∈N* ),数列
(n∈N* ),数列 满足
满足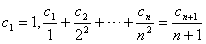 。
。(1)求数列
 、
、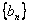 的通项公式;
的通项公式;(2)求数列
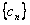 的通项公式;
的通项公式;(3)是否存在正整数k,使得
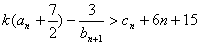 对一切
对一切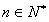 恒成立,若存在求k的最小值;若不存在请说明理由。
恒成立,若存在求k的最小值;若不存在请说明理由。 解:(1)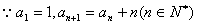 ,
,
∴当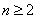 时,
时,
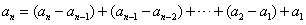
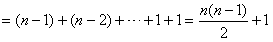
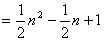 ,
,
∴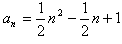
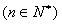 ,
,
又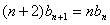
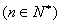 ,
,
∴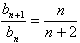 ,
,
∴当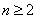 时,
时,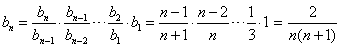 ,
,
∴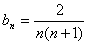 ,
,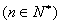 。
。
(2)∵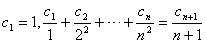 ,
,
∴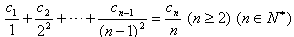 ,
,
两式相减,得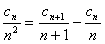 ,
,
∴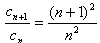 ,
,
又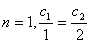 ,
,
∴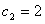 ,
,
∴当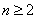 时,
时,
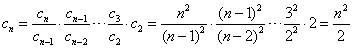 ,
,
∴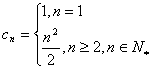 。
。
(3)当n=1时,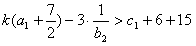 ,
,
∴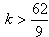 且
且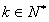 ,即
,即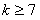 且
且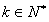 ,
,
当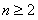 时,
时,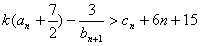 ,
,
即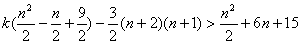 ,
,
化简,得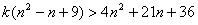 ,
,
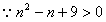 恒成立,
恒成立,
∴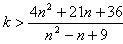 ,
,
事实上,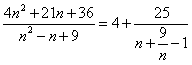 ,
,
又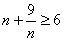 (n=3时,取等号),
(n=3时,取等号),
∴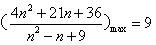 ,
,
∴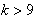 且
且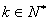 ,
,
综上,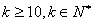 ,
,
所以,k的最小值为10。
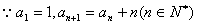 ,
,∴当
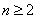 时,
时,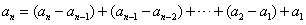
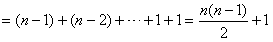
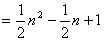 ,
,∴
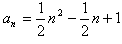
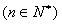 ,
,又
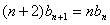
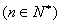 ,
,∴
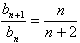 ,
,∴当
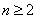 时,
时,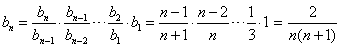 ,
,∴
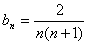 ,
,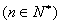 。
。(2)∵
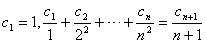 ,
,∴
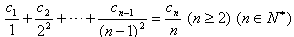 ,
,两式相减,得
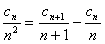 ,
,∴
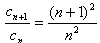 ,
,又
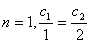 ,
,∴
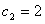 ,
,∴当
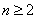 时,
时,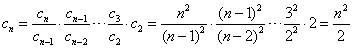 ,
,∴
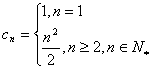 。
。(3)当n=1时,
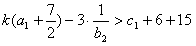 ,
,∴
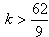 且
且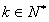 ,即
,即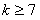 且
且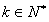 ,
,当
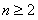 时,
时,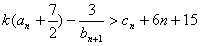 ,
,即
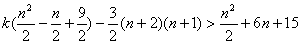 ,
,化简,得
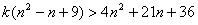 ,
,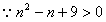 恒成立,
恒成立,∴
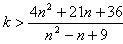 ,
,事实上,
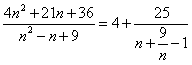 ,
,又
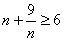 (n=3时,取等号),
(n=3时,取等号),∴
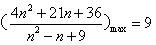 ,
,∴
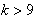 且
且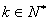 ,
,综上,
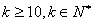 ,
,所以,k的最小值为10。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足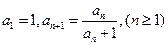 ,数列
,数列 满足
满足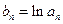 ,数列
,数列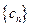
 .
. ,
,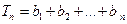 ,试比较
,试比较 与
与 的大小,并证明;
的大小,并证明;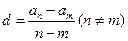 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列 不是一个常数,但
不是一个常数,但 呢,若会,请求出
呢,若会,请求出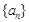 满足:
满足: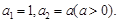 数列
数列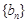 满足
满足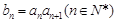 。
。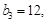 求
求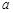 的值及
的值及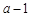 的等比数列时,
的等比数列时,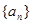 满足
满足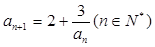 ,数列
,数列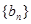 满足
满足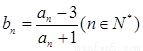 ,
,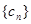 满足
满足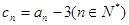 .
.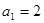 ,证明数列
,证明数列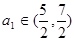 ,证明数列
,证明数列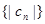 的前
的前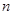 项和
项和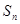 满足
满足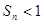 。
。 满足
满足 ,数列
,数列 满足
满足 ,数列
,数列 满足
满足 .
. 与
与 的大小,并说明理由;
的大小,并说明理由; 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列 不是一个常数,但
不是一个常数,但 呢? 若会,求出
呢? 若会,求出 满足:
满足: 数列
数列 满足
满足 .
. 求
求 的值及
的值及 .
.