题目内容
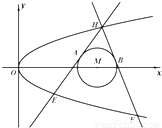
如图,已知抛物线C:y2=2px和⊙M:(x-4)2+y2=1,过抛物线C上一点H(x,y)作两条直线与⊙M相切于A、B两点,分别交抛物线为E、F两点,圆心点M到抛物线准线的距离为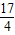 .
. (1)求抛物线C的方程;
(2)当∠AHB的角平分线垂直x轴时,求直线EF的斜率.
【答案】分析:(1)利用点M(4,0)到抛物线准线的距离为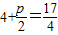 ,即可得出p.
,即可得出p.
(2)当∠AHB的角平分线垂直x轴时,点H(4,2),可得kHE=-kHF,
设E(x1,y1),F(x2,y2),利用抛物线的方程和斜率计算公式即可得出.
解答:解:(1)∵点M(4,0)到抛物线准线的距离为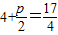 ,
,
∴p= ,即抛物线C的方程为y2=x.
,即抛物线C的方程为y2=x.
(2)∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=-kHF,
设E(x1,y1),F(x2,y2),
∴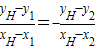 ,
,
∴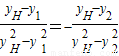 ,
,
∴y1+y2=-2yH=-4.
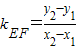 =
=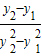 =
=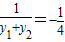 .
.
点评:熟练掌握抛物线的标准方程及其性质、圆的切线的性质、斜率计算公式等是解题的关键.
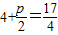 ,即可得出p.
,即可得出p.(2)当∠AHB的角平分线垂直x轴时,点H(4,2),可得kHE=-kHF,
设E(x1,y1),F(x2,y2),利用抛物线的方程和斜率计算公式即可得出.
解答:解:(1)∵点M(4,0)到抛物线准线的距离为
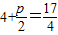 ,
,∴p=
 ,即抛物线C的方程为y2=x.
,即抛物线C的方程为y2=x.(2)∵当∠AHB的角平分线垂直x轴时,点H(4,2),∴kHE=-kHF,
设E(x1,y1),F(x2,y2),
∴
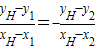 ,
,∴
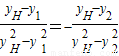 ,
,∴y1+y2=-2yH=-4.
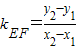 =
=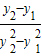 =
=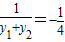 .
.点评:熟练掌握抛物线的标准方程及其性质、圆的切线的性质、斜率计算公式等是解题的关键.

练习册系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且
如图,已知抛物线C:x2=2py(p>0)与圆O:x2+y2=8相交于A、B两点,且 (2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.
(2012•武昌区模拟)如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ. (2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.
(2013•徐州一模)如图,已知抛物线C:y2=4x的焦点为F,过F的直线l与抛物线C交于A(x1,y1)(y1>0),B(x2,y2)两点,T为抛物线的准线与x轴的交点.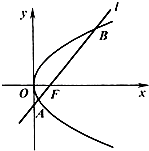 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A、B两点.