题目内容
(本小题12分)
已知圆C: ;
;
(1)若直线 过
过 且与圆C相切,求直线
且与圆C相切,求直线 的方程.
的方程.
(2)是否存在斜率为1直线 ,使直线
,使直线 被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知圆C:
 ;
;(1)若直线
 过
过 且与圆C相切,求直线
且与圆C相切,求直线 的方程.
的方程.(2)是否存在斜率为1直线
 ,使直线
,使直线 被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求出直线
 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.(1) 或
或
(2) 或
或
 或
或
(2)
 或
或
(1)解:圆C可化为: 圆心:
圆心: ;半径:
;半径:
①当 斜率不存在时:
斜率不存在时: ,满足题意……………………………………(2分)
,满足题意……………………………………(2分)
②当 斜率存在时,设斜率为
斜率存在时,设斜率为 ,则:
,则: :
:
则:
故: :
: ………………………………………………(3分)
………………………………………………(3分)
综上之:直线 的方程:
的方程: 或
或 ……………………(1分)
……………………(1分)
(2)解:设直线 的方程:
的方程:
而圆C的圆心: ,则
,则 的中垂线方程是:
的中垂线方程是:
则 的中点
的中点 ……………………………………………(2分)
……………………………………………(2分)
而以 为直径的圆过原点
为直径的圆过原点 ,则:
,则:
即: 或
或 ……(3分)
……(3分)
故所求直线存在,直线 的方程:
的方程: 或
或 ……………(1分)
……………(1分)
 圆心:
圆心: ;半径:
;半径:
①当
 斜率不存在时:
斜率不存在时: ,满足题意……………………………………(2分)
,满足题意……………………………………(2分)②当
 斜率存在时,设斜率为
斜率存在时,设斜率为 ,则:
,则: :
:
则:

故:
 :
: ………………………………………………(3分)
………………………………………………(3分)综上之:直线
 的方程:
的方程: 或
或 ……………………(1分)
……………………(1分)(2)解:设直线
 的方程:
的方程:
而圆C的圆心:
 ,则
,则 的中垂线方程是:
的中垂线方程是:
则
 的中点
的中点 ……………………………………………(2分)
……………………………………………(2分)而以
 为直径的圆过原点
为直径的圆过原点 ,则:
,则:
即:
 或
或 ……(3分)
……(3分)故所求直线存在,直线
 的方程:
的方程: 或
或 ……………(1分)
……………(1分)
练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被 轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线
轴分成两段圆弧,其弧长的比为5∶1.在满足条件(1).(2)的所有圆中,求圆心到直线
 :3
:3 的圆心在直线
的圆心在直线 上,经过点
上,经过点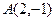 ,且与直线
,且与直线 相切,
相切, 的方程;
的方程;  发出的光线经直线
发出的光线经直线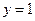 反射后可以照在圆
反射后可以照在圆
 已知关于x,y的方程C:
已知关于x,y的方程C: .
. ,求m的值。
,求m的值。 .若圆
.若圆 的切线在x轴和y轴上截距相等,求切线的方程;
的切线在x轴和y轴上截距相等,求切线的方程; 上恰有三个不同的点到直线
上恰有三个不同的点到直线 的距离为
的距离为 ,则
,则
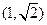 的直线
的直线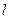 将圆
将圆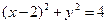 分成两段弧,当劣弧所对的圆心角最小时,直线
分成两段弧,当劣弧所对的圆心角最小时,直线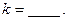
 是一平面图形的直观图,直角边
是一平面图形的直观图,直角边 ,
,



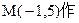 圆
圆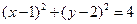 的切线,则切线方程为 ( )
的切线,则切线方程为 ( )


