Question

设函数f（x）=

x2-2(a-1)x+b2

的定义域为D．
（1）a∈{1，2，3，4}，b∈{1，2，3}，求使D=R的概率；
（2）a∈[0，4]，b∈[0，3]，求使D=R的概率．

Answer 1

分析：（1）D=R，等价于x²-2（a-1）x+b²≥0 恒成立，即△=4（a-1）²-4b²≤0，等价于a-1≤b．所有的数对（a，b）共有4×3=12个，而满足条件a-1≤b
的数对用列举法求得共计8个，由此求得D=R的概率．
（2）由（1）可得a-1≤b就行，以a为横坐标，b为纵坐标画图，画出a属于[0，4]，b属于[0，3]的矩形区域OABC，画出b≥a-1的区域，它们相交的部分为
ODBC面积，等于S_OABC-S_△ABD，由此求得D=R的概率．

解答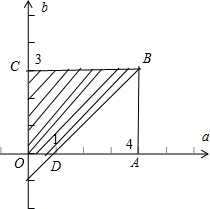：解：（1）D=R，等价于x²-2（a-1）x+b²≥0 恒成立，即△=4（a-1）²-4b²≤0．
因为a、b都是大于零的，所以只要a-1≤b就行．
所有的数对（a，b）共有4×3=12个，而满足条件a-1≤b的数对有（1，1）、（1，2）、
（1，3）、（2，1）、（2，2）、（2，3）、（3，2）、（3，3），共计8个，故D=R的概率为

8

12

=

2

3

．
（2）由（1）可得a-1≤b就行，
以a为横坐标，b为纵坐标画图，画出a属于[0，4]，b属于[0，3]的矩形区域OABC，
画出b≥a-1的区域，它们相交的部分ODBC面积是S_OABC-S_△ABD=12-

1

2

×3×3=

15

2

，
所以D=R的概率是

15 2

12

=

5

8

．

点评：本题考查古典概型及其概率计算公式的应用，简单的线性规划问题，属于基础题．