题目内容
已知函数f(x)=2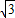 sinx-2cosx.
sinx-2cosx.(Ⅰ)求f(x)的最大值和最小值,及相应的x的取值集合;
(Ⅱ)若f(x)=0,求
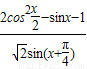 的值.
的值.
【答案】分析:(Ⅰ)利用辅助角公式可求得f(x)=4sin(x-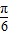 ),利用正弦函数的性质即可求得f(x)的最大值和最小值,及相应的x的取值集合;
),利用正弦函数的性质即可求得f(x)的最大值和最小值,及相应的x的取值集合;
(Ⅱ)由f(x)=0可求得x=kπ+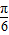 ,k∈Z.化简
,k∈Z.化简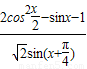 为cot(
为cot(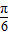 +
+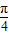 ),利用两角和的正切即可求得答案.
),利用两角和的正切即可求得答案.
解答:解:(Ⅰ)∵f(x)=2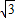 sinx-2cosx=4sin(x-
sinx-2cosx=4sin(x-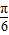 ),
),
∴当x-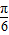 =2kπ+
=2kπ+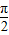 ,即x=2kπ+
,即x=2kπ+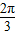 ,(k∈Z)时
,(k∈Z)时
f(x)有最大值,f(x)max=4,
∴f(x)有最大值时x的集合为{x|x=2kπ+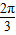 ,k∈Z};
,k∈Z};
当x-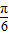 =2kπ-
=2kπ-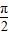 ,即x=2kπ-
,即x=2kπ-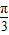 ,(k∈Z)时
,(k∈Z)时
f(x)有最小值,f(x)min=-4;
∴f(x)有最小值时x的集合为{x|x=2kπ-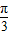 ,k∈Z};
,k∈Z};
(Ⅱ)∵f(x)=0,
∴4sin(x-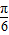 )=0,
)=0,
∴x-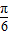 =kπ,
=kπ,
∴x=kπ+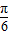 ,k∈Z.
,k∈Z.
∴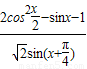
=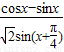
=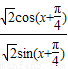
=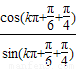
=cot(kπ+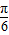 +
+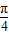 )
)
=cot(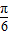 +
+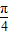 )
)
=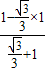 =2-
=2-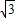 .
.
点评:本题考查三角函数的恒等变换及化简求值,考查正弦函数的最值,考查两角和的正切,属于中档题.
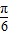 ),利用正弦函数的性质即可求得f(x)的最大值和最小值,及相应的x的取值集合;
),利用正弦函数的性质即可求得f(x)的最大值和最小值,及相应的x的取值集合;(Ⅱ)由f(x)=0可求得x=kπ+
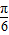 ,k∈Z.化简
,k∈Z.化简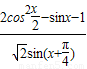 为cot(
为cot(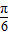 +
+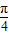 ),利用两角和的正切即可求得答案.
),利用两角和的正切即可求得答案.解答:解:(Ⅰ)∵f(x)=2
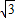 sinx-2cosx=4sin(x-
sinx-2cosx=4sin(x-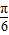 ),
),∴当x-
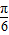 =2kπ+
=2kπ+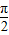 ,即x=2kπ+
,即x=2kπ+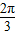 ,(k∈Z)时
,(k∈Z)时f(x)有最大值,f(x)max=4,
∴f(x)有最大值时x的集合为{x|x=2kπ+
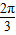 ,k∈Z};
,k∈Z};当x-
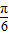 =2kπ-
=2kπ-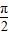 ,即x=2kπ-
,即x=2kπ-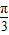 ,(k∈Z)时
,(k∈Z)时f(x)有最小值,f(x)min=-4;
∴f(x)有最小值时x的集合为{x|x=2kπ-
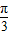 ,k∈Z};
,k∈Z};(Ⅱ)∵f(x)=0,
∴4sin(x-
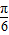 )=0,
)=0,∴x-
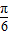 =kπ,
=kπ,∴x=kπ+
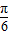 ,k∈Z.
,k∈Z.∴
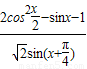
=
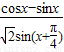
=
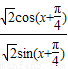
=
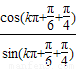
=cot(kπ+
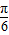 +
+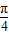 )
)=cot(
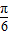 +
+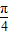 )
)=
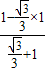 =2-
=2-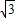 .
.点评:本题考查三角函数的恒等变换及化简求值,考查正弦函数的最值,考查两角和的正切,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目