题目内容
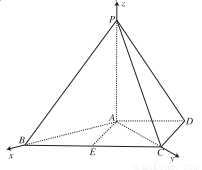
(本小题满分12分)如图,已知四棱锥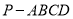 中,
中,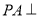 平面
平面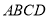 ,
,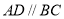 ,
,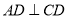 ,且
,且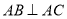 ,
,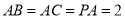 ,
,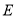 是
是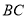 的中点.
的中点.
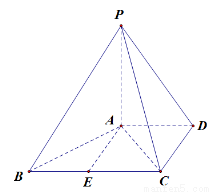
(1)求异面直线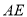 与
与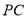 所成角;
所成角;
(2)求二面角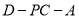 的平面角的余弦值.
的平面角的余弦值.
(1)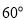 ;(2)
;(2)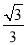 .
.
【解析】
试题分析:(1)分析题意,以 为原点,
为原点, ,
, ,
,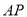 的方向分别作为
的方向分别作为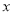 ,
, ,
, 轴的正方向建立空间直角坐标系,分别求出
轴的正方向建立空间直角坐标系,分别求出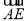 ,
,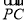 的坐标,计算向量的数量积,求得
的坐标,计算向量的数量积,求得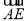 ,
,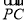 的夹角即可;(2)分别求出平面
的夹角即可;(2)分别求出平面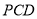 与平面
与平面 的一个法向量,利用法向量即可求得二面角
的一个法向量,利用法向量即可求得二面角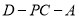 的余弦值.
的余弦值.
试题解析:(1)如图所示,以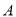 点为原点建立空间直角坐标系
点为原点建立空间直角坐标系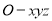 ,则
,则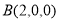 ,
,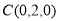 ,
,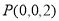 ,故
,故 ,
,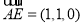 ,
,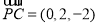 ,
,
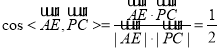 ,即
,即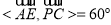 ,故异面直线
,故异面直线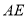 与
与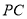 所成角为
所成角为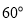 ; (2)在平面
; (2)在平面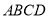 中,∵
中,∵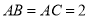 ,
,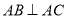 ,∴
,∴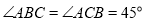 ,
,
∵ ,∴
,∴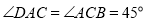 ,由
,由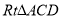 得
得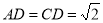 ,∴
,∴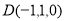 ,
,
又∵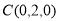 ,∴
,∴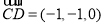 ,
,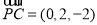 ,设
,设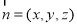 是平面
是平面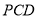 的一个法向量,则
的一个法向量,则 ,
,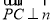 ,即
,即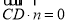 ,
,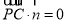 ,∴
,∴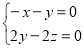 ,令
,令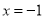 ,得
,得 ,
,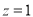 ,即
,即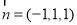 ,
,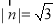 ,又∵
,又∵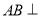 平面
平面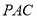 ,∴
,∴ 是平面
是平面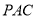 的一个法向量,
的一个法向量,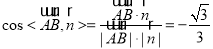 ,即二面角
,即二面角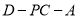 的平面角的余弦值为
的平面角的余弦值为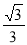 .
.
考点:1.空间向量计算异面直线所成的角;2.空间向量计算二面角的大小.
考点分析: 考点1:异面直线所成的角 考点2:线面所成的角 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
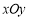 中,已知圆
中,已知圆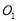 ,圆
,圆 均与
均与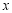 轴相切且圆心
轴相切且圆心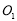 ,
,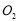 与原点
与原点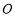 共线,
共线,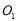 ,
,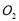 两点的横坐标之积为6,设圆
两点的横坐标之积为6,设圆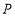 ,
,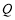 两点,直线
两点,直线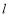 :
: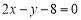 ,则点
,则点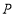 与直线
与直线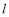 上任意一点
上任意一点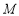 之间的距离的最小值为 .
之间的距离的最小值为 .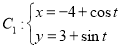 (
(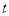 为参数),
为参数),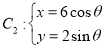 (
(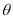 为参数).
为参数).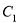 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线; 对应的参数为
对应的参数为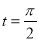 ,
,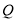 为
为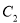 上的动点,求
上的动点,求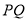 中点
中点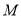 到直线
到直线 (
( ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 (
( 为参数),
为参数), (
( 为参数).
为参数). ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线; 对应的参数为
对应的参数为 ,
, 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
( 的边长为
的边长为 ,
, ,
, ,
, ,则
,则 _______.
_______. ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 ,若对于任意
,若对于任意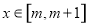 ,都有
,都有 成立,则实数
成立,则实数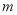 的取值范围是( )
的取值范围是( ) B.
B.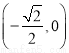 C.
C.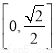 D.
D.
 中,曲线
中,曲线 和
和 的参数方程分别为
的参数方程分别为 为参数
为参数 和
和 为参数
为参数 .以原点
.以原点 为极点,
为极点, 轴正半轴为极轴,建立极坐标系,则曲线
轴正半轴为极轴,建立极坐标系,则曲线