题目内容
已知焦点在y轴,顶点在原点的抛物线C1经过点P(2,2),以C1上一点C2为圆心的圆过定点A(0,1),记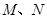 为圆
为圆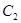 与
与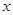 轴的两个交点.
轴的两个交点.
(1)求抛物线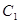 的方程;
的方程;
(2)当圆心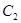 在抛物线上运动时,试判断
在抛物线上运动时,试判断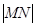 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心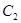 在抛物线上运动时,记
在抛物线上运动时,记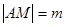 ,
,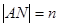 ,求
,求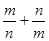 的最大值.
的最大值.
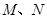 为圆
为圆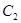 与
与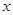 轴的两个交点.
轴的两个交点.(1)求抛物线
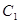 的方程;
的方程;(2)当圆心
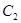 在抛物线上运动时,试判断
在抛物线上运动时,试判断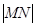 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;(3)当圆心
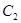 在抛物线上运动时,记
在抛物线上运动时,记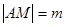 ,
,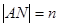 ,求
,求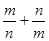 的最大值.
的最大值.(1)x2="2y" ;(2)定值2;(3)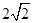
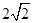
试题分析:(1)由焦点在y轴,顶点在原点的抛物线假设为
 ,又C1经过点P(2,2),即可求出抛物线的
,又C1经过点P(2,2),即可求出抛物线的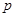 .即可得抛物线的方程.
.即可得抛物线的方程.(2)当圆心
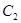 在抛物线上运动时,写出圆
在抛物线上运动时,写出圆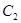 的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.
的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.(3)当圆心
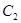 在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心
在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心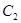 的坐标表示).根据两点的距离公式即可用圆心
的坐标表示).根据两点的距离公式即可用圆心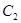 的坐标表示m,n的值,将
的坐标表示m,n的值,将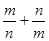 适当变形,再根据基本不等式即可求得
适当变形,再根据基本不等式即可求得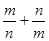 的最大值.
的最大值.(1)由已知,设抛物线方程为x2=2py,22=2p×2,解得p=1.
所求抛物线C1的方程为x2=2y.-------3分
(2)法1:设圆心C2(a,a2/2),则圆C2的半径r=

圆C2的方程为
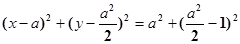 .
.令y=0,得x2-2ax+a2-1=0,得x1=a-1,x2=a+1.
|MN|=|x1-x2|=2(定值).------7分
法2:设圆心C2(a,b),因为圆过A(0,1),所以半径r=
 ,
,,因为C2在抛物线上,a2=2b,且圆被x轴截得的弦长
|MN|=
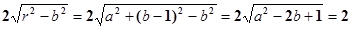 (定值)---7分
(定值)---7分(3)由(2)知,不妨设M(a-1,0),N(a+1,0),
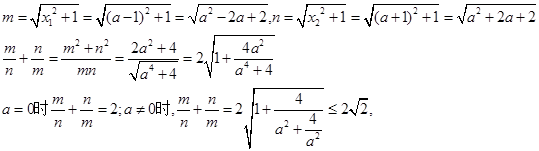


练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 的最大值是 .
的最大值是 .  ,且
,且 ,则
,则 的最小值是_______.
的最小值是_______. 上的函数
上的函数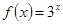 ,若
,若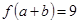 ,则
,则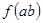 的最大值为______
的最大值为______ +
+ 的最小值是________.
的最小值是________. 若直线
若直线 与直线
与直线 互相垂直,则
互相垂直,则 的
的 且
且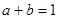 ,则
,则 的最小值为( )
的最小值为( ) ,则
,则 的最小值为_____________.
的最小值为_____________.