题目内容
已知函数![]()
(Ⅰ)若函数![]() 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数![]() 的最小值;
的最小值;
(Ⅱ)方程![]() 有两个不同的实数解,求实数
有两个不同的实数解,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在函数![]() 的图象上是否存在不同两点
的图象上是否存在不同两点![]() ,线段
,线段![]() 的中点的横坐标为
的中点的横坐标为![]() ,有
,有![]() 成立?若存在,请求出
成立?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解(Ⅰ)![]() 1分
1分
若函数![]() 在
在![]() 上递增,则
上递增,则![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,而当
恒成立,而当![]() 时,
时,![]()
![]()
若函数![]() 在
在![]() 上递减,则
上递减,则![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,这是不可能的.
恒成立,这是不可能的.
综上,![]()
![]() 的最小值为1. 4分
的最小值为1. 4分
(Ⅱ)解1、由![]()
令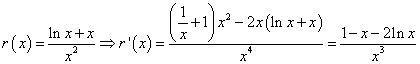
得![]() =0的根为1,所以
=0的根为1,所以
当![]() 时,
时,![]() ,则
,则![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,则
,则![]() 单调递减,
单调递减,
所以![]() 在
在![]() 处取到最大值
处取到最大值![]() ,又
,又![]() ,
,![]() ,
,
所以要使![]() 与
与![]() 有两个不同的交点,则有
有两个不同的交点,则有![]() ……………8分
……………8分
(Ⅲ)假设存在,不妨设![]()
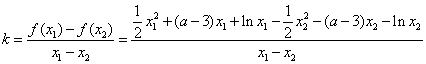
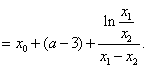 9分
9分
![]()
若![]() 则
则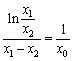 ,即
,即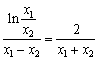 ,即
,即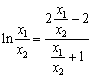 . (*) 12分
. (*) 12分
令![]() ,
,![]() (
(![]() ),
),
则![]() >0.∴
>0.∴![]() 在
在![]() 上增函数, ∴
上增函数, ∴![]() ,
,
∴(*)式不成立,与假设矛盾.∴![]()
因此,满足条件的![]() 不存在. 15分
不存在. 15分

练习册系列答案
相关题目
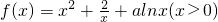 ,
,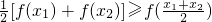 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.