题目内容
【题目】已知椭圆![]() 的右焦点是抛物线
的右焦点是抛物线![]()
![]() 的焦点,直线
的焦点,直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,求
,求![]() 的面积的最小值(
的面积的最小值(![]() 为坐标原点);
为坐标原点);
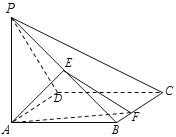
(3)已知点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由题意方程求出右焦点坐标,即抛物线焦点坐标,进一步可得抛物线方程;
(2)设出直线方程,与抛物线方程联立,化为关于y的一元二次方程,利用根与系数的关系求得|y1﹣y2|,代入三角形面积公式,利用二次函数求最值;
(3)分直线AB的斜率存在与不存在,证明有![]() ,可得CA⊥CB,又D为线段AB的中点,则|AB|=2|CD|.
,可得CA⊥CB,又D为线段AB的中点,则|AB|=2|CD|.
(1)∵椭圆![]() 的右焦点为
的右焦点为![]() ,∴
,∴![]() , ∴
, ∴![]() 的方程为
的方程为![]() .
.
(2)(解法1)显然直线![]() 的斜率不为零,设直线
的斜率不为零,设直线![]() 的方程为
的方程为![]() ,
,
由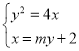 ,得
,得![]() ,则
,则![]() ,
,![]()
![]()
∴当![]() ,即直线
,即直线![]() 垂直
垂直![]() 轴时,
轴时,![]() 的面积取到最小值,最小值为
的面积取到最小值,最小值为![]() .
.
(解法2)若直线![]() 的斜率不存在,由
的斜率不存在,由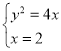 ,得
,得![]() ,
,
![]() 的面积
的面积![]() ,
,
若直线![]() 的斜率存在,不妨设直线
的斜率存在,不妨设直线![]() 的方程为
的方程为![]() ,
,
由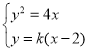 ,得
,得![]() ,
,![]() ,且
,且![]() ,
,![]()
![]() ,
,
即![]() 的面积的最小值为
的面积的最小值为![]() .
.
(3)(解法1)∵直线![]() 的斜率不可能为零,设直线
的斜率不可能为零,设直线![]() 方程为
方程为![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() ,
,![]()
![]() ,
,![]()
∴![]()
![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() 为斜边
为斜边![]() 的中点,所以
的中点,所以![]() .
.
(解法2)(前同解法1)/span>![]()
![]()
线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,![]()
所以![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目