题目内容
如果函数f（x）=ax3-x2+x-5在（-∞，+∞）上单调递增，则实数a的取值范围是（ ）
分析：已知函数f（x）=ax3-x2+x-5在（-∞，+∞）上单调递增，对其进行求导转化成f′（x）＞0在x∈R恒成立，从而求解；
解答：解：∵函数f（x）=ax3-x2+x-5在（-∞，+∞）上单调递增，
∴f′（x）=3ax2-2x+1≥0，在x∈R恒成立，
∴a＞0，△=4-4×3a≥0，
∴a≥
，
故选D．
∴f′（x）=3ax2-2x+1≥0，在x∈R恒成立，
∴a＞0，△=4-4×3a≥0，
∴a≥
| 1 |
| 3 |
故选D．
点评：此题主要考查函数的单调性与导数的关系，将问题转化为二次函数的恒成立，是一道基础题．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
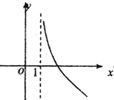
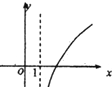
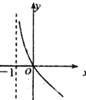
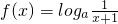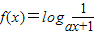的图象大致是
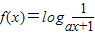的图象大致是（ ）
的图象大致是（ ）
的图象大致是（ ）
