题目内容
(5分)设函数 (a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )
A. [1,e] B. [1,1+e] C. [e,1+e] D. [0,1]
【答案】
A
【解析】由f(f(b))=b,可得f(b)=f﹣1(b)
其中f﹣1(x)是函数f(x)的反函数
因此命题“存在b∈[0,1]使f(f(b))=b成立”,转化为
“存在b∈[0,1],使f(b)=f﹣1(b)”,
即y=f(x)的图象与函数y=f﹣1(x)的图象有交点,
且交点的横坐标b∈[0,1],
∵y=f(x)的图象与y=f﹣1(x)的图象关于直线y=x对称,
∴y=f(x)的图象与函数y=f﹣1(x)的图象的交点必定在直线y=x上,
由此可得,y=f(x)的图象与直线y=x有交点,且交点横坐标b∈[0,1],
根据 ,化简整理得ex=x2﹣x+a
,化简整理得ex=x2﹣x+a
记F(x)=ex,G(x)=x2﹣x+a,在同一坐标系内作出它们的图象,
可得 ,即
,即 ,解之得1≤a≤e
,解之得1≤a≤e
即实数a的取值范围为[1,e]
故选:A


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x,y)使得f(f(y))=y,则a的取值范围是( )
(a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x,y)使得f(f(y))=y,则a的取值范围是( ) (a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是( )
(a∈R,e为自然对数的底数),若曲线y=sinx上存在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是( )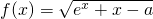 (a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是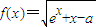 (a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是( )