题目内容

 为非零向量,“函数
为非零向量,“函数 为偶函数”是“
为偶函数”是“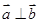 ”的
”的| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
C
分析:已知非零向量

 ,根据f(-x)=f(x),求出向量
,根据f(-x)=f(x),求出向量
 的关系,再利用必要条件和充分条件的定义进行判断.
的关系,再利用必要条件和充分条件的定义进行判断.解:∵函数
 =(|
=(| |x)2+(|
|x)2+(| |)2+2
|)2+2
 x,
x,又f(x)为偶函数,
f(-x)=f(x),
∴f(-x)=(-|
 |x)2+(|
|x)2+(| |)2-2
|)2-2
 x,
x,∴f(-x)=f(x),∴2

 x=0,
x=0,∴

 =0,
=0,∴
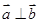 ,
,若
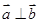 ,则
,则
 =0,∴f(-x)=f(x),
=0,∴f(-x)=f(x),∴f(x)为偶函数,
故选C.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 中,
中, 分别为角
分别为角 的对边,向量
的对边,向量
 ,且
,且 .
. 的大小;
的大小;  ,求
,求 的值.
的值. 的正方形
的正方形 的顶点
的顶点 、
、 分别在
分别在 轴、
轴、 轴(含坐标原点) 上滑动,则
轴(含坐标原点) 上滑动,则 的最大值为( )
的最大值为( )



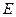 、
、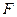 为平面上的两个定点
为平面上的两个定点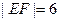 ,
,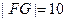 ,且
,且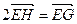 ,
,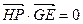 (
( 为动点,
为动点, 是
是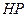 和
和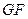 的交点).
的交点).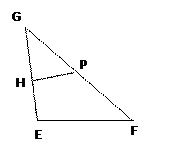
 、
、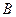 ,且线段
,且线段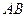 的中垂线与直线
的中垂线与直线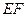 相交于一点
相交于一点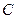 ,证明
,证明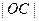 <
<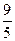 (
(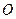 为
为 ,则
,则 为: ( )
为: ( )


 的夹角为
的夹角为 ;则
;则 等于______________.
等于______________. ×
× |=|
|=|
