题目内容
若直线
被圆
截得的弦长为4，则
的最大值是 ．
解析试题分析：圆化为标准方程为：
,所以圆心为
，半径为
，直径为
，又因为直线被圆截得的弦长为4，所以直线过圆心，所以
即
因为
，由基本不等式得
当且仅当
时取等号.
考点：本小题主要考查直线与圆的位置关系的判断、直线过圆心的性质的应用及应用基本不等式求最值，考查学生分析问题、解决问题的能力和运算求解能力.
点评：解决本题的关键在于判断出直线过圆心，从而得到再有就是利用基本不等式求最值要注意“一正二定三相等”三个条件缺一不可.
练习册系列答案
阅读快车系列答案
相关题目
与直线
相切，且圆D与圆C关于直线
对称，则圆D的方程是___________。
为圆上一点，AQ的垂直平分线交CQ于M，则点M的轨迹方程为 。
内点
作圆的两条互相垂直的弦
和
，则
的最大值为 . 
作两条切线，则该圆夹在两条切线间的劣弧长为 .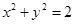
的切线
与
轴的正半轴、
轴的正半轴分别交于点
，当
取最小值时，切线
与曲线
有公共点，那么
的取值范围是