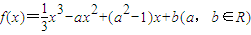题目内容
已知函数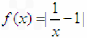
(1)若0<a<b满足f(a)=f(b),求ab的取值范围;
(2 )是否存在正实数a ,b(a<b) ,使得集合{y|y=f(x),a ≤x≤b}=[ma ,mb] ,如果存在,请求出m的取值范围;反之,请说明理由。
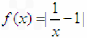
(1)若0<a<b满足f(a)=f(b),求ab的取值范围;
(2 )是否存在正实数a ,b(a<b) ,使得集合{y|y=f(x),a ≤x≤b}=[ma ,mb] ,如果存在,请求出m的取值范围;反之,请说明理由。
解:(1 )∵f(a)=f(b)
∴0<a<1<b且 即
即 ,
,
∴ab>1
(2)∵a<b,ma<mb
∴m>0
当0<a<b≤1时,则 矛盾
矛盾
当0<a<1<b时,∵f(1)=0 [ma,mb]矛盾
[ma,mb]矛盾
当1≤a<b时,则 即
即 
∴ 即mx2-x+1=0在[1,+ ∞)上有两个不等解
即mx2-x+1=0在[1,+ ∞)上有两个不等解
记g(x)=mx2-x+1,则 解得
解得
∴0<a<1<b且
 即
即 ,
, ∴ab>1
(2)∵a<b,ma<mb
∴m>0
当0<a<b≤1时,则
 矛盾
矛盾当0<a<1<b时,∵f(1)=0
 [ma,mb]矛盾
[ma,mb]矛盾当1≤a<b时,则
 即
即 
∴
 即mx2-x+1=0在[1,+ ∞)上有两个不等解
即mx2-x+1=0在[1,+ ∞)上有两个不等解记g(x)=mx2-x+1,则
 解得
解得

练习册系列答案
相关题目