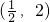Question

若一元二次方程3x²-5x+a=0的一根大于-2且小于0，另一根大于1而小于3，则实数a取值范围（　　）

• A．（-12，0）
• B．(-∞，

  15

  14

  )
• C．(

  15

  14

  ，+∞)
• D．(

  1

  2

  ，2)

Answer 1

分析：设f（x）=3x²-5x+a，根据函数图象可知

f(-2)＞0 f(0)＜0 f(1)＜0 f(3)＞0

，解此不等式组可得实数a的取值范围．

解答：解：设f（x）=3x²-5x+a，
根据函数图象可知

f(-2)＞0 f(0)＜0 f(1)＜0 f(3)＞0

，
即

12+10+a＞0 a＜0 3-5+a＜0 27-15+a＞0

解此不等式组可得a∈（-12，0）
实数a的取值范围：（-12，0）．
故选A

点评：本题主要考查一元二次方程的根的分布与系数的关系和函数与方程思想，函数与方程中蕴涵着丰富的数学思想方法，在解有关函数与方程问题时，应注意数学思想方法的挖掘、提炼、总结，以增强分析问题和解决问题的能力．