题目内容

（2006•广州一模）某学校招收的12名体育特长生中有3名篮球特长生．现要将这12名学生平均分配到3个班中去，每班都分到1名篮球特长生的分配方法共有
10080
10080
种，3名篮球特长生被分配到同一个班的分配方法共有
1890
1890
种．（用数字作答）
分析：对于第一空，需要分三步进行，先将其它9名体育特长生分为3组，由平均分组公式可得其情况数目，再将这三组对应三个班，最后将三名篮球特长生分配到3个班，由排列公式可得其情况数目，由分步计数原理计算可得答案；
对于第二空，也分三步进行，先从其它9名体育特长生中取出1人，与3名篮球特长生组成一组，再将剩余的8名体育特长生分为2组，最后将这三组对应三个班，分别计算每一步的情况数目，由分步计数原理计算可得答案．
解答：解：对于第一空，先将其它9名体育特长生分为3组，有
C
3
9
C
3
6
C
3
3
3!
种情况，
再将这三组对应三个班，有A33种情况，
最后将三名篮球特长生分配到3个班，有A33种情况，
则每班都分到1名篮球特长生的分配方法有
C
3
9
C
3
6
C
3
3
3!
×A33×A33=10800种；
对于第二空，先从其它9名体育特长生中取出1人，与3名篮球特长生组成一组，有C91种情况，
再将剩余的8名体育特长生分为2组，有
C
4
8
C
4
4
2!
种分组方法，
最后将这三组对应三个班，有A33种情况，
则3名篮球特长生被分配到同一个班的分配方法有C91×
C
4
8
C
4
4
2!
×A33=1890种；
故答案为10080，1890．
点评：本题考查排列、组合的运用与分步计数原理的运用，涉及分组问题；注意正确使用平均分组公式即可．
练习册系列答案
相关题目
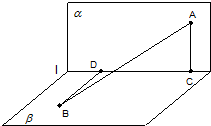（2006•广州一模）如图，长度为2的线段AB夹在直二面角α-l-β的两个半平面内，A∈α，B∈β，
且AB与平面α、β所成的角都是30°，AC⊥l，垂足为C，BD⊥l，垂足为D．
（Ⅰ）求直线AB与CD所成角的大小；
（Ⅱ）求二面角C-AB-D所成平面角的余弦值．
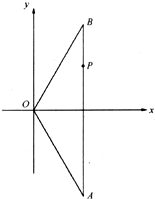（2006•广州一模）如下图，在△OAB中，|OA|=|OB|=4，点P分线段AB所成的比为3：1，以OA、OB所在直线为渐近线的双曲线M恰好经过点P，且离心率为2．
（1）求双曲线M的标准方程；
（2）若直线y=kx+m（k≠0，m≠0）与双曲线M交于不同的两点E、F，且E、F两点都在以Q（0，-3）为圆心的同一圆上，求实数m的取值范围．
（2006•广州一模）函数y=f（x）是定义在R上的增函数，y=f（x）的图象经过点（0，-1）和下面下面的哪一个点时，能使不等式-1＜f（x+1）＜1的解集为{x|-1＜x＜3}（　　）
（2006•广州一模）已知sin
α
2
-cos
α
2
=
5
5
，α∈(
π
2
，π)，tanβ=
1
2
．
（Ⅰ）求sinα的值；
（Ⅱ）求tan（α-β）的值．
（2006•广州一模）记等差数列{an}的前n项和为Sn，若a9=10，则 S17=
170
170
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网