题目内容
【题目】已知圆
，直线
过点
且与圆
相切 .
（I）求直线的方程；
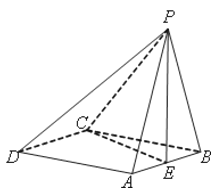
（II）如图，圆与
轴交于
两点，点
是圆上异于
的任意一点，过点
且与轴垂直的直线为
，直线
交直线于点
，直线
交直线于点
，求证：以
为直径的圆
与轴交于定点
，并求出点的坐标 .
【答案】（1）
.
（2）证明见解析；定点
或
.
【解析】
（1）由已知中直线
过点
，我们可以设出直线的点斜式方程，化为一般式方程后，代入点到直线距离公式，根据直线与圆相切，圆心到直线的距离等于半径，可以求出k的值，进而得到直线的方程；
（2）由已知我们易求出P,Q两个点的坐标，设出M点的坐标，我们可以得到点P与Q的坐标，进而得到以
为直径的圆
的方程，根据圆的方程即可判断结论.
(Ⅰ)由题意得，直线的斜率存在.
设直线的方程为
.
因为直线与圆
相切，
所以
.
所以
.
所以直线方程为.
(Ⅱ)由题意得，点
，点
.
设点
，则
.
直线
的方程为
.
所以直线与直线
的交点为点
.
直线
的方程为
.
所以直线与直线的交点为点
.
设点
.
则
，
.
因为以为直径的圆与
轴交于定点
,
所以
解得
.
所以定点或.
名校课堂系列答案
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表所示:
商店名称 | A | B | C | D | E |
销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程
=
x+
,其中=
,=
-
.
(3)若获得利润是4.5百万元时估计销售额是多少(千万元)?
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高 气温 | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | [35, 40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列.
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
