题目内容
用数学归纳法证明某命题时,左式为1-
+
-
+.…+
-
(n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为
-
-
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
分析:分析n=2k、n=2k+2时,左边的式子,即可得到结论.
解答:解:∵n=2k时,左式为1-
+
-
+.…+
-
,
n=2k+2时,左式为1-
+
-
+.…+
-
+
-
,
∴从“n=2k”到“n=2k+2”左边需增加的代数式为
-
故答案为:
-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2k-1 |
| 1 |
| 2k |
n=2k+2时,左式为1-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2k-1 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
∴从“n=2k”到“n=2k+2”左边需增加的代数式为
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
故答案为:
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
点评:本题考查数学归纳法,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
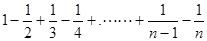 (n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.
(n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.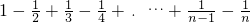 (n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.
(n为正偶数),从“n=2k”到“n=2k+2”左边需增加的代数式为________.