题目内容
在等差数列{an}中,a1=-60,a17=-12,求数列{|an|}的前n项和Tn.
解:数列{an}的公差
d=![]()
∴an=a1+(n-1)d=-60+(n-1)×3=3n-63.
由an<0得,n<21,
∴数列的前20项是负数,第21项及以后的项,都为非负数.
设{an}的前n项和Sn,当n≤20时,
Tn=-Sn=-[-60n+![]() ×3]
×3]
=![]() +
+![]() n;
n;
当n>20时,Tn=-S20+(Sn-S20)=Sn-2S20=-60n+![]() ×3-2(-60×20+
×3-2(-60×20+![]() ×3)
×3)
=![]() -
-![]() n+1 260.
n+1 260.
∴Tn=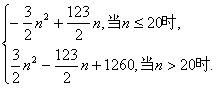

练习册系列答案
相关题目