题目内容
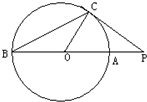
 如图,PC切圆O于点C,割线PAB经过圆心O,PC=4,PB=8,则tan∠COP=________,△OBC的面积是________.
如图,PC切圆O于点C,割线PAB经过圆心O,PC=4,PB=8,则tan∠COP=________,△OBC的面积是________.


分析:利用切割线定理得出PC2=PA•PB,即可解出R.在直角三角形OCP 中,即可得出tan∠COP,sin∠COP,从而得出sin∠BOC,
 .
.解答:∵PC切圆O于点C,根据切割线定理即可得出PC2=PA•PB,∴42=8PA,解得PA=2.
设圆的半径为R,
则2+2R=8,解得R=3.
在Rt△OCP中,
 =
= ,
, .
.∵∠BOC+∠COP=π,∴sin∠BOC=sin(π-∠COP)=
 .
.好∴
 =
= =
= .
.故答案分别为
 ,
, .
.点评:熟练掌握切割线定理、直角三角形的边角关系、三角形的面积计算公式S=
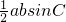 是解题的关键.
是解题的关键. 
练习册系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (几何证明选讲选做题)如图,PC切圆O于点C,割线PAB经过圆O,弦CD⊥AB于点E,已知圆O的半径为3,PA=2,则PC=
(几何证明选讲选做题)如图,PC切圆O于点C,割线PAB经过圆O,弦CD⊥AB于点E,已知圆O的半径为3,PA=2,则PC=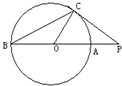 (2013•朝阳区二模)如图,PC切圆O于点C,割线PAB经过圆心O,PC=4,PB=8,则tan∠COP=
(2013•朝阳区二模)如图,PC切圆O于点C,割线PAB经过圆心O,PC=4,PB=8,则tan∠COP= (2012•陕西三模)(考生注意:请在下列三题中任选一题作答,如多做,则按所做的第一题评分)
(2012•陕西三模)(考生注意:请在下列三题中任选一题作答,如多做,则按所做的第一题评分)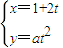 (t为参数,a∈R),点M(5,4)在曲线C 上,则曲线C的普通方程为 .
(t为参数,a∈R),点M(5,4)在曲线C 上,则曲线C的普通方程为 .