题目内容
若函数f（x）=x3-3bx+3b在（0，1）内有极小值，则（ ）A．0＜b＜1
B．b＜1
C．b＞0
D．b＜
【答案】分析：先对函数f（x）进行求导，然后令导函数等于0，由题意知在（0，1）内必有根，从而得到b的范围．
解答：解：因为函数在（0，1）内有极小值，所以极值点在（0，1）上．
令f'（x）=3x2-3b=0，得x2=b，显然b＞0，
∴x=±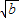
．
又∵x∈（0，1），∴0＜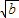
＜1．∴0＜b＜1．
故选A．
点评：本题主要考查应用导数解决有关极值与参数的范围问题．
解答：解：因为函数在（0，1）内有极小值，所以极值点在（0，1）上．
令f'（x）=3x2-3b=0，得x2=b，显然b＞0，
∴x=±
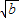．又∵x∈（0，1），∴0＜
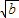＜1．∴0＜b＜1．故选A．
点评：本题主要考查应用导数解决有关极值与参数的范围问题．
练习册系列答案
相关题目