题目内容
中心在原点,焦点在x轴上的椭圆C的离心率为
,且经过点P(1,
).
(1)求C的标准方程;
(2)直线l与C交于A、B两点,M为AB中点,且AB=2MP.请问直线l是否经过某个定点,如果经过定点,求出点的坐标;如果不过定点,请说明理由.
| ||
| 2 |
| ||
| 2 |
(1)求C的标准方程;
(2)直线l与C交于A、B两点,M为AB中点,且AB=2MP.请问直线l是否经过某个定点,如果经过定点,求出点的坐标;如果不过定点,请说明理由.
分析:(1)由 e=
,设C标准方程,代入(1,
),可得a2=2,从而可得C的方程;
(2)若l斜率存在,设l方程为y=kx+b代入椭圆方程整理,利用韦达定理,由AB=2MP得AP⊥PB,即
•
=0,由此可得k,b的关系,从而可得结论;若l斜率不存在,验证即可.
| ||
| 2 |
| ||
| 2 |
(2)若l斜率存在,设l方程为y=kx+b代入椭圆方程整理,利用韦达定理,由AB=2MP得AP⊥PB,即
| PA |
| PB |
解答:解:(1)由 e=
,设C标准方程为
+
=1(a>0)代入(1,
),可得
+
=1,∴a2=2,
∴C的方程为
+y2=1
(2)若l斜率存在,设AB坐标A(x1,y1),B(x2,y2),设l方程为y=kx+b代入椭圆方程整理得:(2k2+1)x2+4kbx+2b2-2=0,∴x1+x2=
,x1x2=
,
由AB=2MP得AP⊥PB,即
•
=0,则(x1-1,y1-
)•(x2-1,y2-
)=0,
即x1x2-(x1+x2)+1+y1y2-
(y1+y2)+
=0∵y1+y2=k(x1+x2)+2b,y1y2=k2x1x2+kb(x1+x2)+b2
代入化简得k2+4kb+3b2-
b-
=0,k=-2b±(b+
),k+b=
或
+b=-
,
若k+b=
,则过定点(1,
),不合题意,舍去;
若
+b=-
,则过定点(
,-
);
若l斜率不存在,通过(
,-
),
综上所述,l通过定点,此点坐标为(
,-
).
| ||
| 2 |
| x2 |
| a2 |
| 2y2 |
| a2 |
| ||
| 2 |
| 1 |
| a2 |
| 1 |
| a2 |
∴C的方程为
| x2 |
| 2 |
(2)若l斜率存在,设AB坐标A(x1,y1),B(x2,y2),设l方程为y=kx+b代入椭圆方程整理得:(2k2+1)x2+4kbx+2b2-2=0,∴x1+x2=
| -4kb |
| (2k2+1) |
| 2b2-2 |
| (2k2+1) |
由AB=2MP得AP⊥PB,即
| PA |
| PB |
| ||
| 2 |
| ||
| 2 |
即x1x2-(x1+x2)+1+y1y2-
| ||
| 2 |
| 1 |
| 2 |
代入化简得k2+4kb+3b2-
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| k |
| 3 |
| ||
| 6 |
若k+b=
| ||
| 2 |
| ||
| 2 |
若
| k |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
若l斜率不存在,通过(
| 1 |
| 3 |
| ||
| 6 |
综上所述,l通过定点,此点坐标为(
| 1 |
| 3 |
| ||
| 6 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查分类讨论的数学思想,正确运用韦达定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
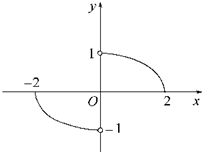 如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-2≤x<-
| ||||||||
C、{x|-2≤x<-
| ||||||||
D、{x|-
|
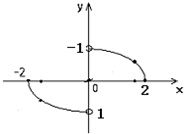 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
 .
.