Question

已知p：x²-8x-48≤0，q：x²-2x+1-a²≤0（a＞0）．若p是q的充分不必要条件，求实数a的取值范围．

Answer 1

分析：结合不等式的解法，先求出p，q成立的等价条件，利用p是q的充分不必要条件即可求解a的取值范围．

解答：解：∵x²-8x-48≤0，
∴（x-12）（x+8）≤0，
即-8≤x≤12．即p：-8≤x≤12．
∵x²-2x+1-a²≤0（a＞0）．
∴[x-（1-a）][x-（1+a）]≤0，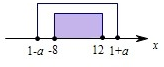
∴1-a≤x≤1+a．（a＞0）
即q：1-a≤x≤1+a．（a＞0）．
∵p是q的充分不必要条件，
∴

1+a≥12 1-a≤-8

，
即

a≥11 a≥9

，
∴a≥11，
∴实数a的取值范围是a≥11．

点评：本题主要考查充分条件和必要条件的应用，利用不等式的解法先求出p，q的等价条件是解决本题的关键．利用数轴是解决此类问题的基本方法．