题目内容
已知某几何体的直观图和三视图如下图所示,其正视图、侧视图均为直角三角形,俯视图为直角梯形。
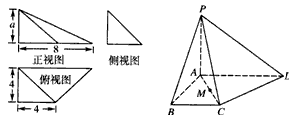
(1)M为AC中点,证明:BM⊥平面PAC:
(2)设直线PD与平面PAC所成的角的正弦值为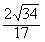 ,求过P-ACD的外接球的体积。
,求过P-ACD的外接球的体积。
(2)设直线PD与平面PAC所成的角的正弦值为
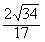 ,求过P-ACD的外接球的体积。
,求过P-ACD的外接球的体积。| 解:(1)证明:由三视图可知PA⊥平面ABCD, 即BM⊥PA, 又AB=BC,且M是AC的中点, 即BM⊥AC, 所以BM⊥平面PAC。 |
|
| (2)连接BM延长交AD于E,即E为AD的中点, 又取PA中点为F,连接MF,EF∥PD, 即PD与平面PAC所成的角,转化为EF与平面PAC 所成的角, ∠MFE为EF与平面PAC所成的角,  , , 又AC⊥CD,PA⊥CD, 所以PC⊥CD 过P-ACD的外接球的球心为PD的中点, 外接球的半径  外接球体积为  。 。 |
 |

练习册系列答案
相关题目





