题目内容

（2013•泰安一模）已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB=8，BC=2
3
，则棱锥O-ABCD的体积为
16
2
16
2
．
分析：根据题意，球心0在矩形所在平面内的射影为矩形对角线的交点O1．算出AC=
AB 2+BC 2
=2
19
，结合球的截面圆性质算出OO1=
6
，最后利用锥体体积公式即可算出棱锥O-ABCD的体积．
解答：解：球心0在矩形所在平面内的射影为矩形对角线的交点O1．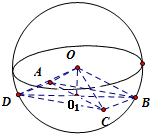
∵AB=8，BC=2
3
，
∴对角线长AC=
82+(2
3
)2
=2
19
，
由球的截面圆性质，得
棱锥的高OO1=
52-(
19
)2
=
6
，
∴棱锥O-ABCD的体积为V=
1
3
SABCD×OO1=
1
3
×
6
×8×2
3
=16
2
．
故答案为：16
2
点评：本题给出圆的内接矩形ABCD，求棱锥O-ABCD的体积．着重考查了球的截面圆性质和锥体体积公式等知识，属于中档题．
练习册系列答案
相关题目
（2013•泰安一模）已知集合A={-1，1}，B={x|1≤2x＜4}，则A∩B等于（　　）
（2013•泰安一模）设奇函数f（x）在[-1，1]上是增函数，f（-1）=-1．若函数f（x）≤t2-2at+1对所有的x∈[-1，1]都成立，则当a∈[-1，1]时，t的取值范围是（　　）
（2013•泰安一模）若a，b∈R，且ab＞0，则下列不等式中，恒成立的是（　　）
（2013•泰安一模）某产品按行业生产标准分成6个等级，等级系数ξ依次为1，2，3，4，5，6，按行业规定产品的等级系数ξ≥5的为一等品，3≤ξ＜5的为二等品，ξ＜3的为三等品．
若某工厂生产的产品均符合行业标准，从该厂生产的产品中随机抽取30件，相应的等级系数组成一个样本，数据如下；

（I）以此30件产品的样本来估计该厂产品的总体情况，试分别求出该厂生产原一等品、二等品和三等品的概率；
（II）已知该厂生产一件产品的利润y（单位：元）与产品的等级系数ζ的关系式为y=
1，ξ＜3
2，3≤ξ＜5
4，ξ≥5
，若从该厂大量产品中任取两件，其利润记为Z，求Z的分布列和数学期望．
（2013•泰安一模）已知函数f（x）=（ax2+bx+c）ex且f（0）=1，f（1）=0．
（I）若f（x）在区间[0，1]上单调递减，求实数a的取值范围；
（II）当a=0时，是否存在实数m使不等式2f（x）+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立？若存在，求出m的值，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网