题目内容
经过一点只能有一条直线和一个平面垂直.
已知：一点A和平面α.
求证：经过点A只能有一条直线和平面α垂直.
证明：根据点A和平面α的位置关系，分两种情况证明.
(1)如图(1)所示，点A在平面α内.假设经过点A至少有平面α的两条垂线AB、AC，那么AB、AC是两条相交直线，它们确定一个平面β，平面β和平面α相交于经过点A的一条直线a.
因为AB⊥平面α，AC⊥平面α，a
α,
所以AB⊥a,AC⊥a,在平面β内经过A有两条垂线都和直线a垂直，这与平面几何中经过直线上一点只能有已知直线的一条垂线相矛盾.
(2)如图(2)所示，点A在平面α外，假设经过点A至少有平面α的两条垂线AB和AC(B、C为垂足)，那么AB、AC是两条相交直线，它们确定一个平面β，平面β和平面α相交于直线BC.因为AB⊥平面α，AC⊥平面α,BC
α，所以AB⊥BC，AC⊥BC.
在平面β内经过点A有两条直线都和BC垂直，与平面几何中经过直线外一点只能有已知直线的一条垂线相矛盾.
综上，经过一点A只能有平面α的一条垂线.
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
内有且仅有一条直线和这个平面
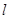垂直
内有且仅有一条直线和这个平面外的一条直线l垂直。