Question

已知函数f（x）=

1

3

x³-（a-1）x²+b²x，其中a，b为实常数．
（Ⅰ）求函数f（x）为奇函数的充要条件；
（Ⅱ）若任取a∈[0，4]，b∈[0，3]，求函数f（x）在R上是增函数的概率．

Answer 1

分析：（Ⅰ）由函数f（x）为奇函数得到f（-x）=-f（x），代入函数解析式，得到恒成立的方程，整理对应相等，即可求得常数a的值；（Ⅱ）函数f（x）在R上是增函数转化为f'（x）≥0恒成立，∴△≤0解得a，b的一个关系式，根据a∈[0，4]，b∈[0，3]，画出图象，即可求得函数f（x）在R上是增函数的概率．

解答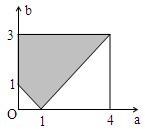：解：（Ⅰ）若f（x）任意x∈R，
有f（x）+f（-x）=0
即

1

3

x3-(a-1)x2+b2x-

1

3

x3-(a-1)x2-b2x=0
∴2（a-1）x²=0∴a=1
当a=1 时，f(x)=

1

3

x3+b2x
f(-x)=-

1

3

x3-b2x=-f(x)，所以f（x）为奇函数．
故f（x）为奇函数的充要条件是a=1．

（Ⅱ）因为f'（x）=x²-2（a-1）x+b²．
若f（x）在R上是增函数，则对任意x∈R，f'（x）≥0恒成立．
所以△=4（a-1）²-4b²≤0，即|a-1|＜|b|．
设“f（x）在R上是增函数”为事件A，则事件A对应的区域为{（a，b）||a-1|＜|b|}．
又全部试验结果Ω=（a，b）|0≤a≤4，0≤b≤3，如图．
所以P(A)=

S图象

SΩ

 =

3×4- 1 2 ×1×1- 1 2 ×3×3

3×4

=

7

12

．
故函数f（x）在R上是增函数的概率为

7

12

．

点评：（Ⅰ）考查函数的奇偶性的定义，以及方程的思想方法求参数的值，特别注意函数的定义域；（Ⅱ）考查利用导数研究函数的单调性，转化为恒成立问题求解，是导数与几何概型相结合的题目，新颖，体现了数形结合的思想，属中档题．