题目内容

           已知椭圆的对称点落在直线）上，且椭圆C的离心率为

   （1）求椭圆C的方程；

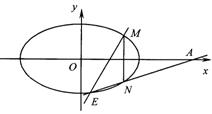
   （2）设A（3，0），M、N是椭圆C上关于x轴对称的任意两点，连结AN交椭圆于另一点E，求证直线ME与x轴相交于定点.

（1）     （2）直线ME与x轴相交于定点（，0）


解析:

（1）

       设O关于直线的对称点为，

       则的横坐标为

       又易知直线O的方程为

       为（1，－3）.

       ∴椭圆方程为

   （2）显然直线AN存在斜率，设直线AN的方程为

       并整理得：

       设点

       由韦达定理得

       ∵直线ME方程为的横坐标

       将

       再将韦达定理的结果代入，并整理可得

       ∴.

练习册系列答案
相关题目
精英家教网如图，在直角坐标系xOy中，已知椭圆C：
y2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的
直线与椭圆C相交M、N两点，且|MN|=1．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设椭圆C的左顶点为A，下顶点为B，动点P满足
PA
•
AB
=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．
在直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率e=
2
2
，左右两个焦分别为F1，F2．过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点，且|MN|=2．
（1）求椭圆C的方程；
（2）设椭圆C的一个顶点为B（0，-b），是否存在直线l：y=x+m，使点B关于直线l 的对称点落在椭圆C上，若存在，求出直线l的方程，若不存在，请说明理由．

（08年威海市模拟理）（12分）已知椭圆的对称点落在直线）上，且椭圆C的离心率为

   （1）求椭圆C的方程；

   （2）设A（3，0），M、N是椭圆C上关于x轴对称的任意两点，连结AN交椭圆于另一点E，求证直线ME与x轴相交于定点.

 

（12分）已知椭圆的离心率为，椭圆的中心关于直线的对称点落在直线上

(1)求椭圆C的方程；

(2)设是椭圆上关于轴对称的任意两点，连接交椭圆于另一点，求直线的斜率范围并证明直线与轴相交顶点。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网