题目内容
已知函数f（x）=lg（x2+1）的值域为M，函数g（x）=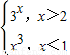
，的定义域N，则M∩N=（ ）A．[0，1）
B．（2，+∞）
C．[1，+∞）
D．[0，1）∪（2，+∞）
【答案】分析：根据题意求出M与N，进而求出交集即可．
解答：解：∵x2+1≥1，∴f（x）=lg（x2+1）≥0，即M=[0，+∞），
∵g（x）的定义域N=（-∞，1）∪（2，+∞），
∴M∩N=[0，1）∪（2，+∞）．
故选D
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
解答：解：∵x2+1≥1，∴f（x）=lg（x2+1）≥0，即M=[0，+∞），
∵g（x）的定义域N=（-∞，1）∪（2，+∞），
∴M∩N=[0，1）∪（2，+∞）．
故选D
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目