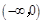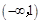题目内容
函数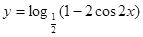 的一个单调递减区间是( )
的一个单调递减区间是( )
A. | B.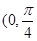 ) ) |
C.[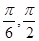 ] ] | D.[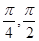 ] ] |
D
解析试题分析:令t=1-2cos2x,则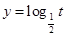 在
在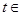 (0,+
(0,+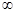 )为减函数,所以为求
)为减函数,所以为求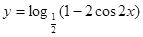 的一个单调递减区间,须t>0,且t=1-2cos2x为增函数, 所以
的一个单调递减区间,须t>0,且t=1-2cos2x为增函数, 所以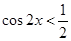 ,且
,且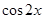 为减函数。即
为减函数。即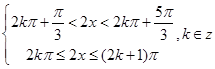 ,
,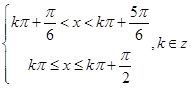 ,所以
,所以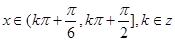 ,故选D。
,故选D。
考点: 复合函数的单调性,对数函数、余弦函数的性质。
点评:中档题,复合函数的单调性判断应遵循内外层函数“同增异减”。要特别注意函数的定义域。

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
已知函数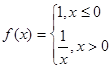 ,则使方程
,则使方程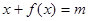 有解的实数
有解的实数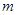 的取值范围
的取值范围
是( )
| A.(1,2) | B. | C.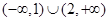 | D.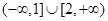 |
若函数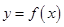 为偶函数,则函数
为偶函数,则函数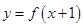 的一条对称轴是
的一条对称轴是
A.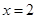 | B.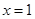 | C.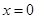 | D.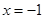 |
函数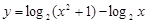 的值域是
的值域是
A.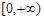 | B.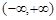 |
C.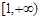 | D.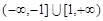 |
 是定义在
是定义在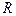 上的以3为周期的偶函数,且
上的以3为周期的偶函数,且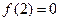 ,则方程
,则方程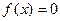 在区间
在区间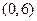 内解的个数的最小值是 ( )
内解的个数的最小值是 ( )
| A.5 | B.4 | C.3 | D.2 |
已知函数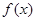 是R上的单调减函数且为奇函数,则
是R上的单调减函数且为奇函数,则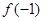 的值( )
的值( )
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
函数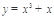 的递增区间是( )
的递增区间是( )
A.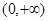 | B.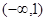 | C.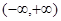 | D.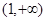 |
定义在R上的偶函数
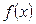 满足:对任意的
满足:对任意的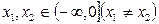 ,有
,有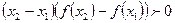 .则当
.则当 时,有网Z.X.X.K]
时,有网Z.X.X.K]
A.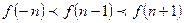 | B.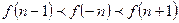  | C.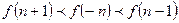 | D.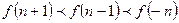 |
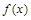 都满足不等式
都满足不等式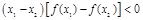 ,若函数
,若函数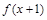 为奇函数,则不等式
为奇函数,则不等式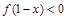 的解集为 ( )
的解集为 ( )