题目内容
极坐标方程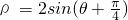 的图形是
的图形是
- A.

- B.

- C.

- D.

C
分析:先将原极坐标方程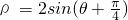 中的三角函数式利用和角公式展开,再两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行判断.
中的三角函数式利用和角公式展开,再两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行判断.
解答:将原极坐标方程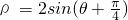 ,化为:
,化为:
ρ= sinθ+
sinθ+ cosθ
cosθ
ρ2= ρsinθ+
ρsinθ+ ρcosθ
ρcosθ
化成直角坐标方程为:x2+y2- y-
y- x=0,
x=0,
它表示圆心在第一象限,半径为1的圆.
故选C.
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.
分析:先将原极坐标方程
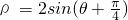 中的三角函数式利用和角公式展开,再两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行判断.
中的三角函数式利用和角公式展开,再两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行判断.解答:将原极坐标方程
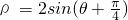 ,化为:
,化为:ρ=
 sinθ+
sinθ+ cosθ
cosθρ2=
 ρsinθ+
ρsinθ+ ρcosθ
ρcosθ化成直角坐标方程为:x2+y2-
 y-
y- x=0,
x=0,它表示圆心在第一象限,半径为1的圆.
故选C.
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目


 =2sin(
=2sin( +
+ )的图形是(
)
)的图形是(
)
 的图形是( )
的图形是( )


