题目内容
已知函数F(x)=ax﹣lnx(a>0)
(1)若曲线y=f(x)在点(l,f(l))处的切线方程为y=2x+b,求a,b的值;
(2)若当x∈[l,e]时,函数f(x)的最小值是4,求函数f(x)在该区间上的最大值.
(1)若曲线y=f(x)在点(l,f(l))处的切线方程为y=2x+b,求a,b的值;
(2)若当x∈[l,e]时,函数f(x)的最小值是4,求函数f(x)在该区间上的最大值.
解:(1)求导函数,可得f′(x)=a﹣  (x>0)
(x>0)
由f′(1)=a﹣1=2,∴a=3
∴f(1)=3
∴b=f(1)﹣2×1=1
(2)定义域为(0,+∞),f′(x)=a﹣ =
= 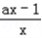
由f′(x)>0,得x> ,f′(x)<0,得0<x<
,f′(x)<0,得0<x<
∴f(x)在(0, )上单调递减,在(
)上单调递减,在( 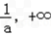 )单调递增
)单调递增
若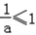 ,即a≥1时,f(x)在[1,e]单调递增,
,即a≥1时,f(x)在[1,e]单调递增,
∴f(x)min=f(1)=a=4,此时f(x)max=f(e)=4e﹣1
若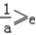 ,即0<a≤
,即0<a≤ 时,f(x)在[1,e]单调递减,
时,f(x)在[1,e]单调递减,
∴f(x)min=f(e)=ae﹣1=4,∴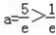 (不合题意)
(不合题意)
若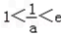 ,即
,即 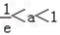 时,f(x)在(1,
时,f(x)在(1, )单调递减,在(
)单调递减,在(  ,e)单调递增,
,e)单调递增,
∴f(x)min=f( )=1+lna=4 此时a=e3(不合题意)
)=1+lna=4 此时a=e3(不合题意)
综上知,f(x)max=4e﹣1
 (x>0)
(x>0)由f′(1)=a﹣1=2,∴a=3
∴f(1)=3
∴b=f(1)﹣2×1=1
(2)定义域为(0,+∞),f′(x)=a﹣
 =
= 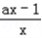
由f′(x)>0,得x>
 ,f′(x)<0,得0<x<
,f′(x)<0,得0<x<
∴f(x)在(0,
 )上单调递减,在(
)上单调递减,在( 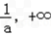 )单调递增
)单调递增若
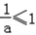 ,即a≥1时,f(x)在[1,e]单调递增,
,即a≥1时,f(x)在[1,e]单调递增,∴f(x)min=f(1)=a=4,此时f(x)max=f(e)=4e﹣1
若
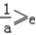 ,即0<a≤
,即0<a≤ 时,f(x)在[1,e]单调递减,
时,f(x)在[1,e]单调递减,∴f(x)min=f(e)=ae﹣1=4,∴
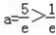 (不合题意)
(不合题意)若
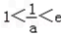 ,即
,即 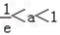 时,f(x)在(1,
时,f(x)在(1, )单调递减,在(
)单调递减,在(  ,e)单调递增,
,e)单调递增,∴f(x)min=f(
 )=1+lna=4 此时a=e3(不合题意)
)=1+lna=4 此时a=e3(不合题意)综上知,f(x)max=4e﹣1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目