题目内容
(1)x,y∈R,x+y=5,求3x+3y的最小值.
(2)若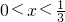 时,求函数y=x(1-3x)的最大值.
时,求函数y=x(1-3x)的最大值.
解:(1)由3x>0,3y>0,
∴3x+3y≥2 =18
=18 
所以3x+3y的最小值为18 ,
,
当且仅当,3x=3y,x=y= 时,取等号.
时,取等号.
(2)∵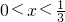 ,∴3x>0,1-3x>0,
,∴3x>0,1-3x>0,
∴y=x(1-3x)=

当且仅当3x=1-3x即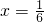 时取“=”号
时取“=”号
分析:(1)首先判断3x>0,3y>0,然后知3x+3y≥2 =18
=18  .
.
(2)先根据x的范围确定1-3x的符号,再由y=x(1-3x)= 结合基本不等式的内容可得到函数的最大值.
结合基本不等式的内容可得到函数的最大值.
点评:本题考查均值不等式的性质和应用,解题时要注意公式的正确应用,应用基本不等式时注意“一正、二定、三相等”的原则.
∴3x+3y≥2
 =18
=18 
所以3x+3y的最小值为18
 ,
,当且仅当,3x=3y,x=y=
 时,取等号.
时,取等号.(2)∵
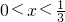 ,∴3x>0,1-3x>0,
,∴3x>0,1-3x>0,∴y=x(1-3x)=


当且仅当3x=1-3x即
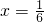 时取“=”号
时取“=”号分析:(1)首先判断3x>0,3y>0,然后知3x+3y≥2
 =18
=18  .
.(2)先根据x的范围确定1-3x的符号,再由y=x(1-3x)=
 结合基本不等式的内容可得到函数的最大值.
结合基本不等式的内容可得到函数的最大值.点评:本题考查均值不等式的性质和应用,解题时要注意公式的正确应用,应用基本不等式时注意“一正、二定、三相等”的原则.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目