题目内容
已知函数f(x)=
x3+ax2+(2a-1)x.
(1)若f'(-3)=0,求a的值;
(2)若a>1,求函数发f(x)的单调区间与极值点;
(3)设函数g(x)=f'(x)是偶函数,若过点A(1,m)(m≠-
)可作曲线y=f(x)的三条切线,求实数m的取值范围.
| 1 |
| 3 |
(1)若f'(-3)=0,求a的值;
(2)若a>1,求函数发f(x)的单调区间与极值点;
(3)设函数g(x)=f'(x)是偶函数,若过点A(1,m)(m≠-
| 2 |
| 3 |
f′(x)=x2+2ax+2a-1
(1)∵f'(-3)=0,∴9-6a+2a-1=0,
解得:a=2;
(2)f'(x)=(x+1)(x+2a-1),
∵a>1,由f'(x)=(x+1)(x+2a-1)>0
得x<1-2a或x>-1,所以f(x)的单调增区间为(-∞,1-2a)和(-1,+∞);
由f'(x)=(x+1)(x+2a-1)<0得1-2a<x<-1,
所以f(x)的单调减区间为(1-2a,-1);
且x=1-2a是极大值点,x=-1是极小值点;
(3)∵g(x)=f'(x)是偶函数,
∴a=0
∴f(x)=
x3 -x,设曲线线 过点A(1,m)(m≠-
)的切线相切于点P(x0,
x03-x0 ),
则切线的斜率 k=x02-1,
∴切线方程为y-(
x03-x0)═(x02-1)(x-x0),
∵点A(1,m)在切线上,
∴m-(
x03-x0)=(x02-1)(1-x0),
解得m=-
x03+x02-1
令h(x)=-
x 3+x 2-1,
则h′(x)=-2x2+2x=2x(1-x)=0,解得x=0,x=1当x=0时,
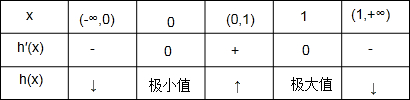
h(x)去极小值-1,当x=1时,h(x)去极大值-
,
∴实数m的取值范围是-1<m<-
.
(1)∵f'(-3)=0,∴9-6a+2a-1=0,
解得:a=2;
(2)f'(x)=(x+1)(x+2a-1),
∵a>1,由f'(x)=(x+1)(x+2a-1)>0
得x<1-2a或x>-1,所以f(x)的单调增区间为(-∞,1-2a)和(-1,+∞);
由f'(x)=(x+1)(x+2a-1)<0得1-2a<x<-1,
所以f(x)的单调减区间为(1-2a,-1);
且x=1-2a是极大值点,x=-1是极小值点;
(3)∵g(x)=f'(x)是偶函数,
∴a=0
∴f(x)=
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
则切线的斜率 k=x02-1,
∴切线方程为y-(
| 1 |
| 3 |
∵点A(1,m)在切线上,
∴m-(
| 1 |
| 3 |
解得m=-
| 2 |
| 3 |
令h(x)=-
| 2 |
| 3 |
则h′(x)=-2x2+2x=2x(1-x)=0,解得x=0,x=1当x=0时,

h(x)去极小值-1,当x=1时,h(x)去极大值-
| 2 |
| 3 |
∴实数m的取值范围是-1<m<-
| 2 |
| 3 |

练习册系列答案
相关题目